4. K-최근접 이웃 알고리즘 (K-Nearest Neighbor)
K-최근접 이웃K-Nearest Neighbor:KNN 알고리즘을 활용하여 분류와 회귀 문제를 해결할 수 있다.
KNN 알고리즘은 특정 입력 데이터 x에 대해, 주변 k개의 데이터의 클래스 중 가장 많은 클래스로 특정 자료를 분류하는 방식이다.

학습 데이터 자체가 모델이 되어, 따로 추정 방법이나 파라메터를 필요로 하지 않는다. 이 떄문에 KNN은 매우 간단하고 저사양이지만, 높은 정확도를 보여준다.
이 때문에 KNN은 게으른 학습Lazy Learner, 사례 중심 학습Instance-Based Learning이라 불린다.
이는 훈련 데이터로부터 판별 함수Discriminative Function를 학습하지 않고, 훈련 데이터 셋을 메모리에 저장하여 사용하는 방법을 말한다.
차원의 저주Curse of Dimension
KNN은 데이터의 차원이 증가할 수록 성능 저하가 심해지는데, 데이터의 차원이 증가할수록 데이터가 이루는 공간의 부피가 기하급수적으로 증가하여, 동일한 개수의 데이터 밀도가 희박sparse해지기 때문이다. (즉, 더 많은 데이터가 필요하다.)
차원이 증가할 수록 훨씬 더 많은 데이터를 필요로 하게 되는데, 이를 차원의 저주라 한다.
민코프스키 거리Minkowski Distance: 데이터 간의 거리 측정 방법
데이터 간의 거리를 비교하는 방법으로는 민코프스키 거리를 이용한다.
$$d(x_i, x_j) = ^P\sqrt{\Sigma^d_{k=1} \mid x_{ik}-x_{jk} \mid ^P} $$
이때, $P$가 1이면 맨하탄 거리(L1 거리), 2이면 유클리디언 거리(L2 거리)가 된다는 점에 주목하자.
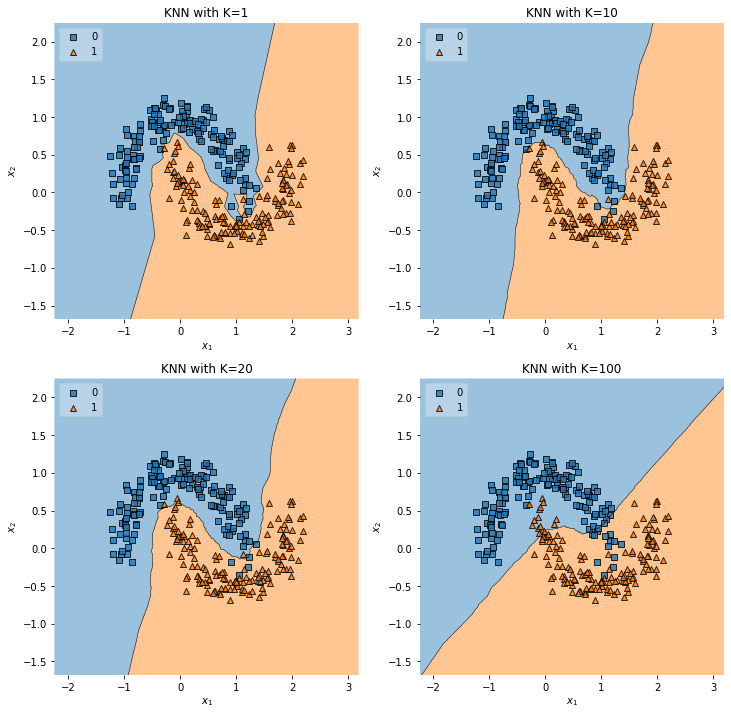
KNN의 오버피팅과 언더피팅
KNN의 하이퍼 파라메터 $k$를 몇으로 잡느냐에 따라, KNN에서 오버피팅이나 언터피팅이 발생한다.
$k$가 너무 작을 경우, 데이터의 지역적 특성을 지나치게 반영하여 과적합이 발생하고, 너무 크게 잡으면, 모델이 과하게 관대해져, 언더피팅이 발생한다.
다수결 방식Majority Voting과 가중합 방식Weighted Voting
KNN은 대표적인 다수결 방식 알고리즘이다. $k$개의 이웃 가운데, 빈도를 기준으로 클래스를 반영한다.
반면, 가중합 방식 알고리즘에서는 가까운 이웃에 더 가중치를 부여하여 클래스를 판별한다.
KNN의 장단점
KNN 알고리즘의 장점은 아래와 같다.
- 학습 데이터의 노이즈에 크게 영향을 받지 않는다.
- 학습 데이터의 수가 충분하다면, 상당히 좋은 성능을 낸다.
- 마할라노비스 거리 등 데이터의 분산까지 고려하면 상당히 강건robust해진다.
- 마할라노비스 거리Mahalanobis Distance는 평균과의 거리가 표준편차의 몇 배인지를 나타낸 값이다.
- 즉, 이 데이터가 얼마나 표준에서 벗어난 값인지를 수치화하는 방법이다.
반면, KNN 알고리즘의 단점은 다음과 같다.
- 최적 이웃의 수($k$)와 사용할 거리 척도를 데이터 각각의 특성에 맞게 연구자가 임의로 설정해줘야 한다.
- 이는 데이터에따라 다르기에, Grid Search를 통해 찾아줘야 한다. (즉, 대학원생이 노가다를 해야한다.)
- 새로운 관측치와 각 학습 데이터 사이의 거리를 전부 측정해야 하므로, 계산 시간이 오래 걸린다.
- 이를 완화하기 위해, Locality Sensitive Hashing, Network based Indexer, Optimized Product Quantization 등이 시도되었다.
실습: 붓꽃 데이터 분류
붓꽃 데이터셋(IRIS)를 활용한 실습 코드는 제 깃허브에서 확인하실 수 있습니다.
github.com/skyil7/SejongUniv_ML/blob/master/2.KNN.ipynb
skyil7/SejongUniv_ML
Sejong University Machine Learning. Contribute to skyil7/SejongUniv_ML development by creating an account on GitHub.
github.com
KNN을 이용한 회귀 문제
KNN을 이용하여 클래스를 분류하는 것 뿐 아니라, 회귀 문제도 풀 수 있다.
최근접한 $k$개의 이웃들의 결과값의 평균을 사용하거나, 가중합한 후 평균을 구하여 회귀 문제에 KNN을 적용할 수 있다.
KNN을 활용한 IMDb 별점 회귀 문제 실습 코드:
github.com/skyil7/SejongUniv_ML/blob/master/2.5.KNN%20regression.ipynb
skyil7/SejongUniv_ML
Sejong University Machine Learning. Contribute to skyil7/SejongUniv_ML development by creating an account on GitHub.
github.com