DnS: Distill-and-Select for Efficient and Accurate Video Indexing and Retrieval 리뷰 (IJCV 2022)
이 논문은 당시 Video Retrieval SOTA 모델인 ViSiL이 성능은 높지만, 매우 많은 연산을 요구하여 속도가 느린 점을 해결하고자 knowledge distillation과 Selector 모델을 활용한다.
Video Retrieval에는 속도가 빠르지만 정확도가 떨어지는 video-level 방법(coarse-grained)과 속도가 느리지만 정확도가 높은 frame-level 방법(fine-grained)이 있는데, DnS는 먼저 video-level 모델 하나와 frame-level 모델 두 개를 student 모델로 두고, ViSiL을 teacher 모델 삼아 knowledge distillation을 수행한다.
그다음, 추론 단계에서 속도가 빠른 video-level student로 기본적인 검색을 수행하되, 속도가 느리더라도 더욱 정확한 frame-level student를 사용해야 할지 판단하여, 필요한 경우 frame-level student를 사용하도록 하는 selector network를 학습시켜 필요에 따라 video-level 혹은 frame-level 방법을 선택하여 사용하도록 한다.
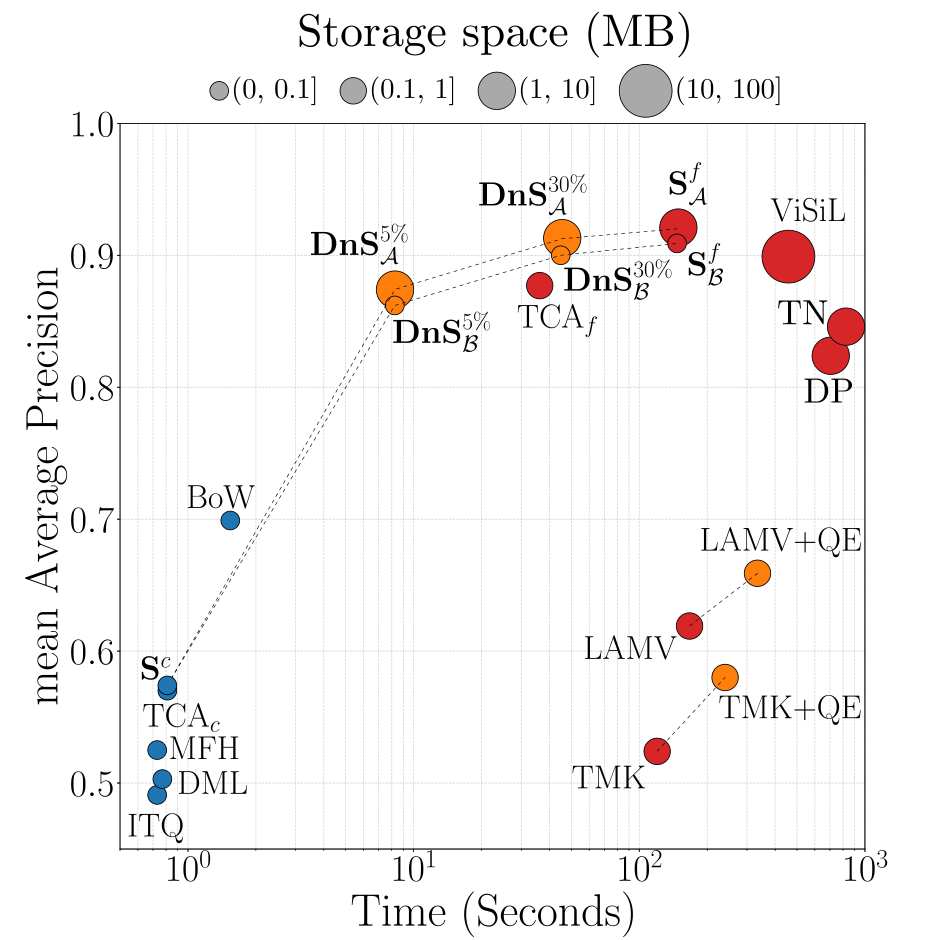
이렇게 video-level 방법과 frame-level 방법을 선택적으로 조합하는 re-ranking 방법을 통해, DnS는 높은 정확도와 기존 frame-level 방법들에 비해 상대적으로 빠른 검색 시간을 가질 수 있었다.
DnS: Distill and Select 구조
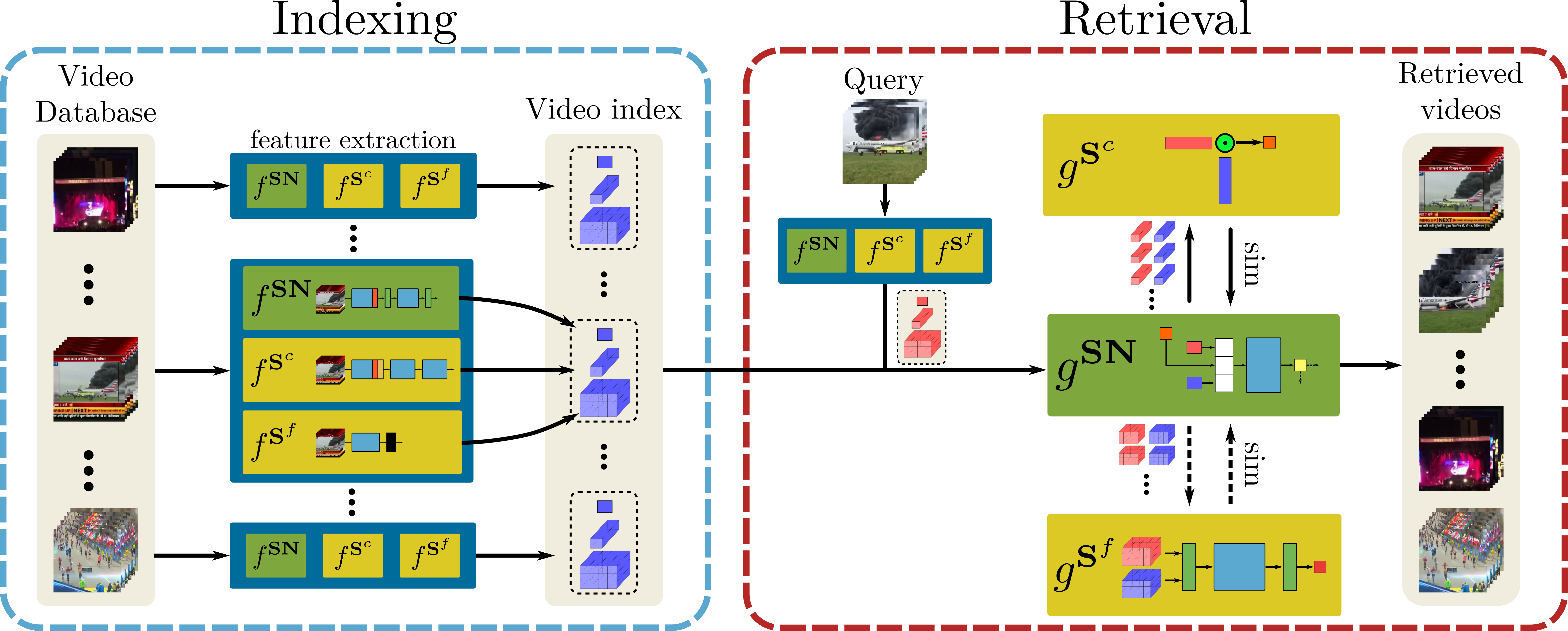
DnS 모델은 다음과 같은 3개의 sub network로 구성된다.
- 매우 빠르지만 정확도가 낮은 video-level 모델 $S^c$
- 속도는 느리지만 정확도가 높은 frame-level 모델 $S^f$
- 두 검색 모델 중 어떤 모델을 사용할지 결정하는 Selector Network $SN$
Database의 각 영상은 다음과 같은 세 가지 정보를 저장하고 있다.
- $S^c$가 생성한 global 1D tensor
- $S^f$가 생성한 spatio-temporal 3D tensor
- $SN$이 추출한 Self Similarity Scalar
DnS의 영상 검색 과정은 다음과 같다.
- 먼저, 쿼리 영상을 $S^c$에 입력하여 $g^{S^c}$를 얻는다.
- $g^{S^c}$를 $SN$에 입력하여 $S^f$를 사용할지 결정하는 binary decision $g^{SN}$을 얻는다.
- 만약 $S^f$를 사용한다면, 쿼리 영상을 $S^f$에 입력하여 $g^{S^f}$를 얻고, DB의 영상들과 frame-level로 비교를 수행한다.
- 그렇지 않다면, $g^{S^c}$를 DB 영상들과 video-level로 비교한다.
Network Architectures
Baseline Teacher ($T$)
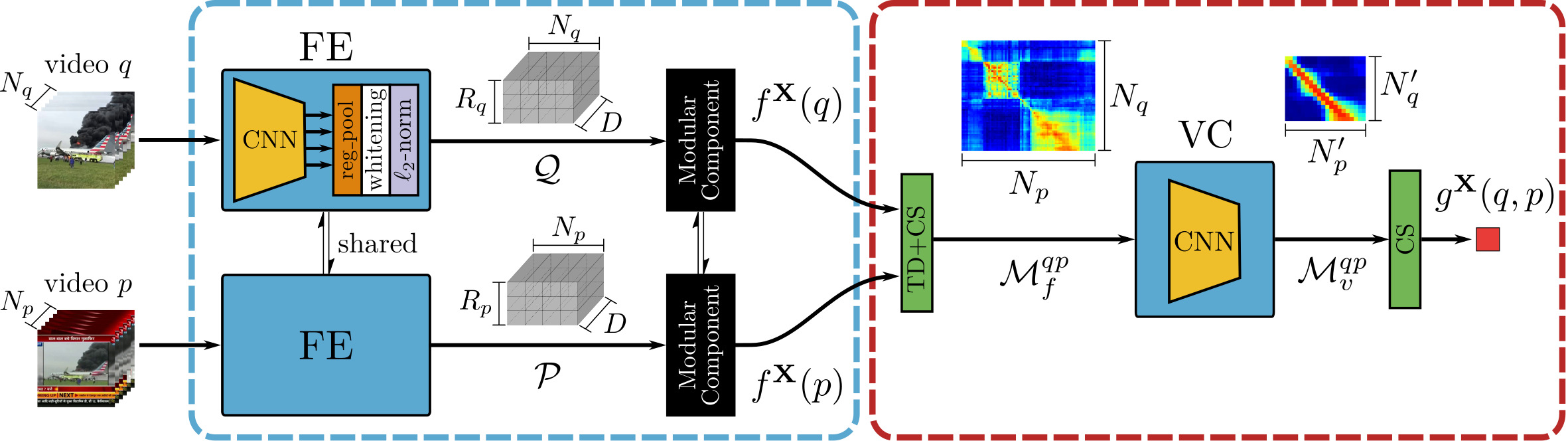
teacher 모델로는 ViSiL을 사용한다. (ViSiL 리뷰)
ViSiL은 영상의 각 프레임에서 L3-iMAC을 추출하여 $\mathcal{X} \in \mathbb {R}^{N\times R\times D}$의 video descriptor tensor를 얻는다. 이때, $N$은 프레임의 수, $R$은 각 프레임에서 추출하는 영역의 수(L3-iMAC에서 9), $D$는 각 region 벡터의 크기이다. 추출한 feature에서 각 region 벡터에 학습 가능한 $D$차원의 벡터를 이용해 $l^2$ attention을 적용한다.
저자들은 이러한 indexing 과정을 $f^T(x)$로 나타내었다.
teacher 모델의 유사도 계산 역시, ViSiL의 것을 그대로 가져왔다. Tensor Dot 연산과 Chamfer Similarity 연산을 통해 각 프레임의 유사도를 region 단위로 비교하여 구하여 frame-to-frame similarity map을 만들고, 이를 Video Comparator (VC)라고 하는 신경망에 넣어 refinement 한 다음, 다시 Chamfer Similarity를 구해 영상 간의 유사도 $g^T(q, p)$를 얻는다.
Fine-grained Attention Student ($S^f_\mathcal{A}$)
저자들은 두 가지 frame-level student를 만들었는데 이 모델은 Teacher 모델인 ViSiL과 매우 유사한 구조로 되어있다. 때문에 연산량은 거의 비슷하지만, Knowledge Distillation 과정에서 대량의 unlabeled data로 학습되기 때문에 Teacher Model인 ViSiL보다 높은 정확도를 달성할 수 있었다고 한다.
Indexing 과정 $f^{S^f_\mathcal{A}}$는 ViSiL과 거의 유사하나, Attention 가중치를 부여할 때 학습 가능한 $D$차원의 벡터를 이용한 $l^2$ 어텐션이 아닌, h-어텐션을 수행한다. 먼저 선형 계층에 region vector를 입력해 hidden vector $h$를 만들고, tanh로 활성화 함수를 적용해 준다. 그리고 context vector $u$를 곱하여 다시 시그모이드를 태워준 후, 가중치를 적용한다. 식으로 나타내면 아래와 같다.
$$ h= \tanh(r\cdot W_a + b_a) \\
\alpha = \text{sig}(u\cdot h) \\
r' = \alpha r$$
결과적으로, 이 모델 역시 ViSiL과 같은 3차원 텐서 서술자를 만든다.
유사도 계산 과정인 $g^{S^f_\mathcal{A}}$ 역시 ViSiL과 완전히 동일하게 수행된다.
Fine-grained Binarization Student ($S^f_\mathcal{B}$)
이 모델 역시 frame-level 방법으로, ViSiL과 비슷한 구조, 비슷한 연산량을 갖지만 어텐션 대신 binarization을 수행하여 feature의 크기를 크게 줄였다. 덕분에 훨씬 좋은 저장 공간 효율성을 가지며, Distillation 과정에서 더 많은 데이터로 학습될 경우 역시 Teacher 모델인 ViSiL보다 좋은 정확도를 보인다고 한다.
Indexing 과정 $f^{S^f_\mathcal{B}}$에서 어텐션을 수행하는 대신, region vector $r$에 학습 가능한 가중치 $W_\mathcal{B} \in \mathbb{R}^{D\times L}$를 곱한 후, 이진화 함수 $\text{sgn}(r\cdot W_\mathcal{B})$를 적용하여 $-1, 1$ 중 하나의 값을 갖도록 한다. 이진화 함수는 미분이 불가하기 때문에, 학습 시에는 이진화 함수에 근사하는 함수를 대신 사용한다. 그러므로, 학습 단계에서 이진화 모듈의 기댓값은 아래 식과 같다. $\mu$는 x가 유도되는 단변량 가우시안 분포의 평균이며 $\sigma^2$는 고정된 분산이다.
$$\mathbb{E}[\text{sgn}(x)] = \text{erf}(\frac{\mu}{\sqrt{2\sigma ^2}})$$
$\text{erf]()$는 에러 함수로 미분 가능한 함수이기에 활성화 함수로 사용할 수 있다. 결과적으로, 이진화 함수는 아래와 같다.
$$ b(r) = \text{erf}(\frac{r\cdot W_\mathcal{B}}{\sqrt{2\sigma^2}})$$
유사도 계산 과정 $g^{S^f_\mathcal{B}}$에서는 Chamfer Similarity와 Hamming Similarity를 결합하여 사용한다.
Coarse-grained Student ($S^c$)
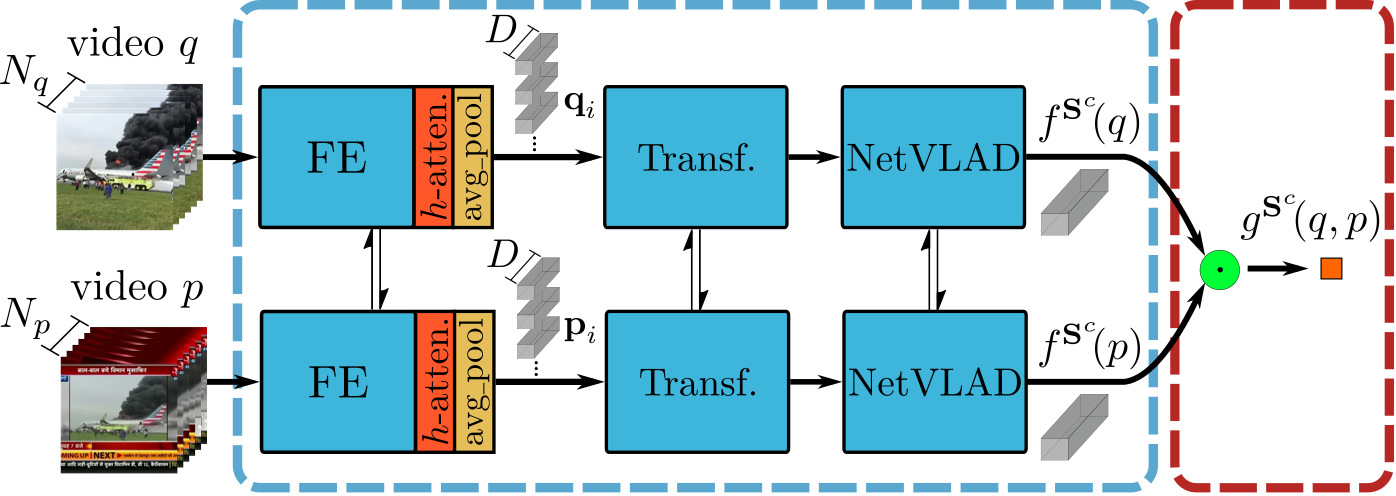
이 모델은 video-level 방법으로 retrieval을 수행하여, teacher 모델이나 다른 student들에 비해 훨씬 적은 저장공간과 연산량을 요구한다. 그러나 그만큼 정확도 역시 낮다고 한다.
Indexing 과정 $f^{S^c}$는 다음과 같은 과정으로 수행된다.
- $S^f_\mathcal{A}$와 같은 방식으로 어텐션을 부여한 영상의 L3-iMAC feature 추출
- 공간축에 대해 average pooling을 수행하여 각 프레임에 대한 feature가 $D$차원의 벡터가 되도록 만듦
- 트랜스포머 인코더 구조를 활용해 frame-level feature들의 long-term dependency들을 병합 (TCA)
- NetVLAD 모듈을 통해 전체 feature를 하나의 벡터로 병합
ViSiL과 TCA, NetVLAD를 융합한 방식으로 video-level student의 성능을 최대한 끌어올리려고 했음을 느낄 수 있다.
영상 유사도 계산 $g^{S^c}$는 벡터 간의 닷 연산을 통해 쉽게 수행할 수 있다.
Selector Network ($SN$)
추론 단계에서 쿼리 영상이 입력되면, 먼저 속도가 빠른 $S^c$를 통해 모든 영상과의 유사도가 계산된다. 이때, $SN$은 이렇게 구한 유사도를 사용하는 것이 적절한지, 혹은 더 정확한 유사도를 시간을 들여 구해야 할지 판단한다.
이때, $SN$은 다음 세 가지 값을 입력받는다.
- $S^c$로 계산한 두 영상의 video-level 유사도 $g^{S^c}$
- 비교하고자 하는 두 영상의 Self Similarity $f^{SN}$
$SN$은 각 영상이 얼마나 큰 spatio-temporal 다양성을 갖는지를 나타내는 self-similarity를 구할 수 있다. 이때, $S^f_\mathcal{A}$와 같은 방식으로 frame-level feature $\mathcal{X} \in \mathbb{R}^{N\times R\times D}$를 추출하여, 아래 식을 통해 프레임 간 self-similarity를 구한다.
$$ \mathcal{M}_f^x = \frac{1}{R^2}\sum^{R}_{i=1}\sum^{R}_{j=1} \mathcal{X}\cdot_{(3,1)} \mathcal{X}^\mathsf{T}(\cdot, i, j, \cdot )$$
복잡해 보이지만, Chamfer Similarity 연산 대신 평균 연산을 적용한 것으로, 프레임들이 서로 얼마나 유사한지 평균을 구하는 것이다. 이어서, ViSiL과 유사하게 Video Comparator CNN에 이 유사도 행렬을 입력하고, 최종적으로 다시 평균을 구하여, 영상의 self-similarity를 얻는다.
영상의 self-similarity가 낮다면, 영상의 spatio-temporal 다양성이 크다는 것이고, self-similarity가 높다면 영상의 다양성이 적다는 것이다. 영상의 다양성이 적다면 그만큼 frame들이 대체로 비슷하다는 것이고, 굳이 frame-level로 비교를 수행할 필요가 없다는 것이 $SN$의 가설이다.
앞서 언급한 것처럼, video-level 유사도 $g^{S^c}$와 비교할 두 영상의 self-similarity를 MLP 구조의 이진 분류기에 넣어 frame-level student의 사용 여부를 결정한다.
학습 과정
먼저, Teacher Model인 ViSiL은 VCDB와 같은 labeled video dataset에서 triplet loss를 통해 학습한다. 그 다음, 저자들이 논문에서 제안하는 DnS-100K와 같은 대규모의 unlabeled dataset에 대하여 Teacher 모델이 예측을 수행하고, Student 모델들은 이 예측을 pseudo label 삼아 학습한다.
이때, teacher model로 데이터셋의 모든 영상 쌍에 대한 예측을 수행하기에는 비용이 너무 커지므로, 한 양성 쌍에 대하여 다른 앵커에 대응되는 영상 50개와, 아무 쿼리와도 관련이 없는 방해자 영상 50개를 선정하여 이들에 대한 유사도를 계산해놓고 사용하였다.
Selector Network $SN$은 $S^c$와 $S^f$로 구한 유사도의 차이가 임계값 이상인 영상 쌍들을 분류하도록 이진 교차 엔트로피 손실로 학습된다.
Implementation Details
Teacher의 학습에는 VCDB 데이터셋을 사용하고, Student에 대한 knowledge distillation은 논문에서 제안한 unlabeled dataset인 DnS-100K 데이터셋을 사용하였다. $S^f_\mathcal{B}$의 이진화 계층에는 DnS에서 추출한 백만 개의 region vector로 학습된 ITQ 알고리즘을 사용하여 초기화를 진행했다고 한다.
Experiments
Retrieval Performance of Individual Networks
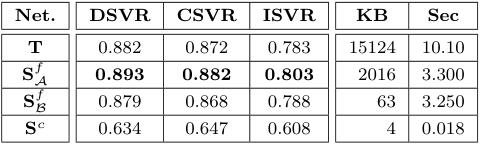
각 신경망을 단독으로 사용하였을 때, Teacher model ViSiL $T$와 유사한 구조를 가지면서 DnS-100K에서 distillation된 $S^f_\mathcal{A}$가 가장 좋은 성능을 보였으며, 속도도 ViSiL보다 빨랐다.
이진화를 사용하는 $S^f_\mathcal{B}$는 훨씬 적은 저장공간을 사용함에도 $T$와 거의 유사한 성능을 보이며, 심지어 ISVR에서는 $T$보다 높은 성능을 보였다.
$S^c$는 역시 가장 부족한 성능을 보였지만, 압도적으로 적은 저장공간을 사용하고 검색 속도도 빨랐다.
Distillation vs Supervision
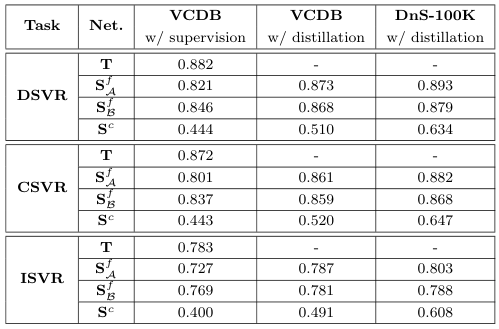
저자들은 각 모델을 teacher와 동일하게 VCDB에서 지도학습하는 경우와, VCDB 혹은 DnS-100K에서 distillation한 경우의 성능을 비교하였다.
전반적으로 Distillation을 사용하는 것이 성능을 향상했으며, 특히 VCDB의 near-duplicate보다 더 다양하고 많은 데이터를 포함한 DnS-100K에서 distillation을 수행하는 것이 성능을 크게 향상했다.
Impact of dataset size
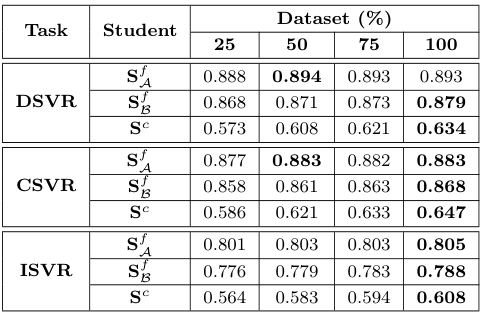
저자들은 Knowledge Distillation 과정에서 사용되는 DnS-100K 데이터셋의 비율을 조절하며, 데이터의 양과 성능의 관계를 분석하였다. $S^f_\mathcal{B}$와 $S^c$의 경우, 학습 데이터의 양에 따른 성능의 차이가 크게 나타났다. 반면에 $S^f_\mathcal{A}$는 학습 데이터의 양이 변화하여도 결과가 비교적 안정적이었는데, 이는 입력 feature를 변형하지 않고 사용하는 $S^f_\mathcal{A}$가 다른 모델들에 비해 더 강건하게 학습한 것으로 생각된다고 한다.
Student performance with different teachers
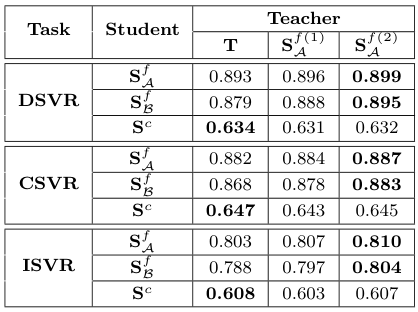
앞서, Student 모델들이 Teacher 모델인 ViSiL에 비해 한층 성능이 높은 모습을 보였는데, 이렇게 $T$로 학습한 모델 $S^{f(1)}_\mathcal{A}$과, 이 모델로 다시 학습한 모델 $S^{f(2)}_\mathcal{A}$를 사용해 Distillation을 수행해 보았다.
신기하게도, fine-grained student들의 성능은 이에 따라 꽤 크게 상승하였다. 그러나 $S^c$는 성능이 상승하지 않았다.
Student performance with different settings
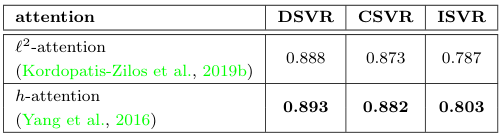
$S^f_\mathcal{A}$에 적용하는 어텐션을 기존 ViSiL이 사용하던 $l^2$ 어텐션과 h 어텐션 사이에서 비교해 보았다. h 어텐션의 성능이 전체적으로 더 높았기에, 논문에서는 h 어텐션을 사용하였다.
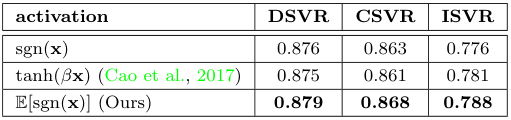
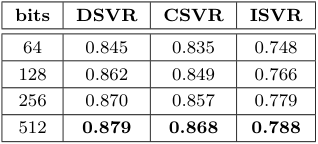
$S^f_\mathcal{B}$의 이진화 계층에 사용하는 활성화 함수의 비교를 진행하였다. 그 결과, 저자들이 사용한 함수가 가장 좋은 성능을 보였으며, 나아가 이진화에 사용되는 비트 수를 비교하였을 때, 비트가 많을수록 성능이 향상됐다.
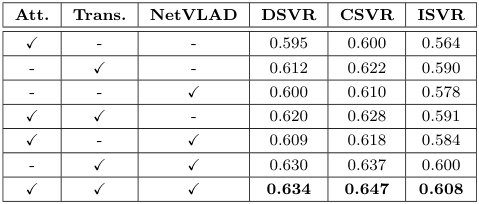
Coarse-grained Student $S^c$의 각 모듈에 대하여 Ablation Study를 실시한 결과, 모든 모듈이 존재하는 것이 가장 높은 성능을 보였다. 위 표에 아무 모듈도 없는 경우도 있었으면 좋았을 것 같은데, 없는 이유는 의문이다....
Selector Network Performance
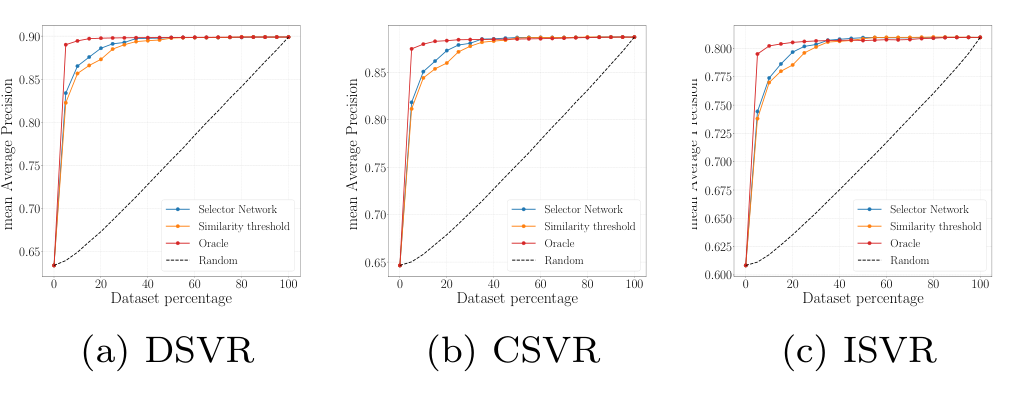
정확도가 낮은 $S^c$를 사용할지, $S^f$를 사용할지 판단하는 기준에 따른 성능을 분석하였다. $S^c$와 $S^f$가 생성하는 유사도를 알고 있는 경우를 의미하는 당연히도 Oracle이 가장 높은 정확도를 내었고, selector network를 사용하는 방법이 뒤를 이었다. 단순히 유사도 thresholding을 진행하는 경우, 가장 안 좋은 성능이 나타났다.
Impact of threshold on the selector performance
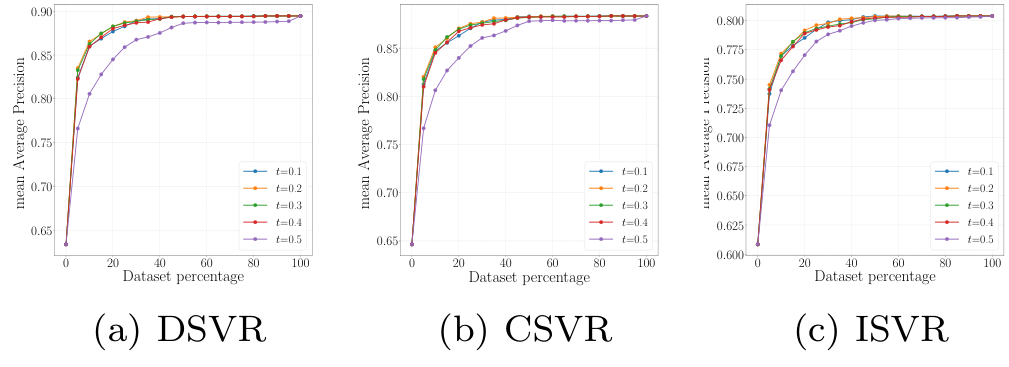
Selector Network 학습에 사용되는 threshold 값 설정에 따른 성능 비교를 수행하였다. t=0.2로 설정한 경우가 가장 성능이 좋았으나, 0.1~0.4 사이의 성능이 사실 대부분이 비슷하였다. 다만 t가 0.4를 넘자 성능이 급격히 하락하였다.
Comparison with SOTA
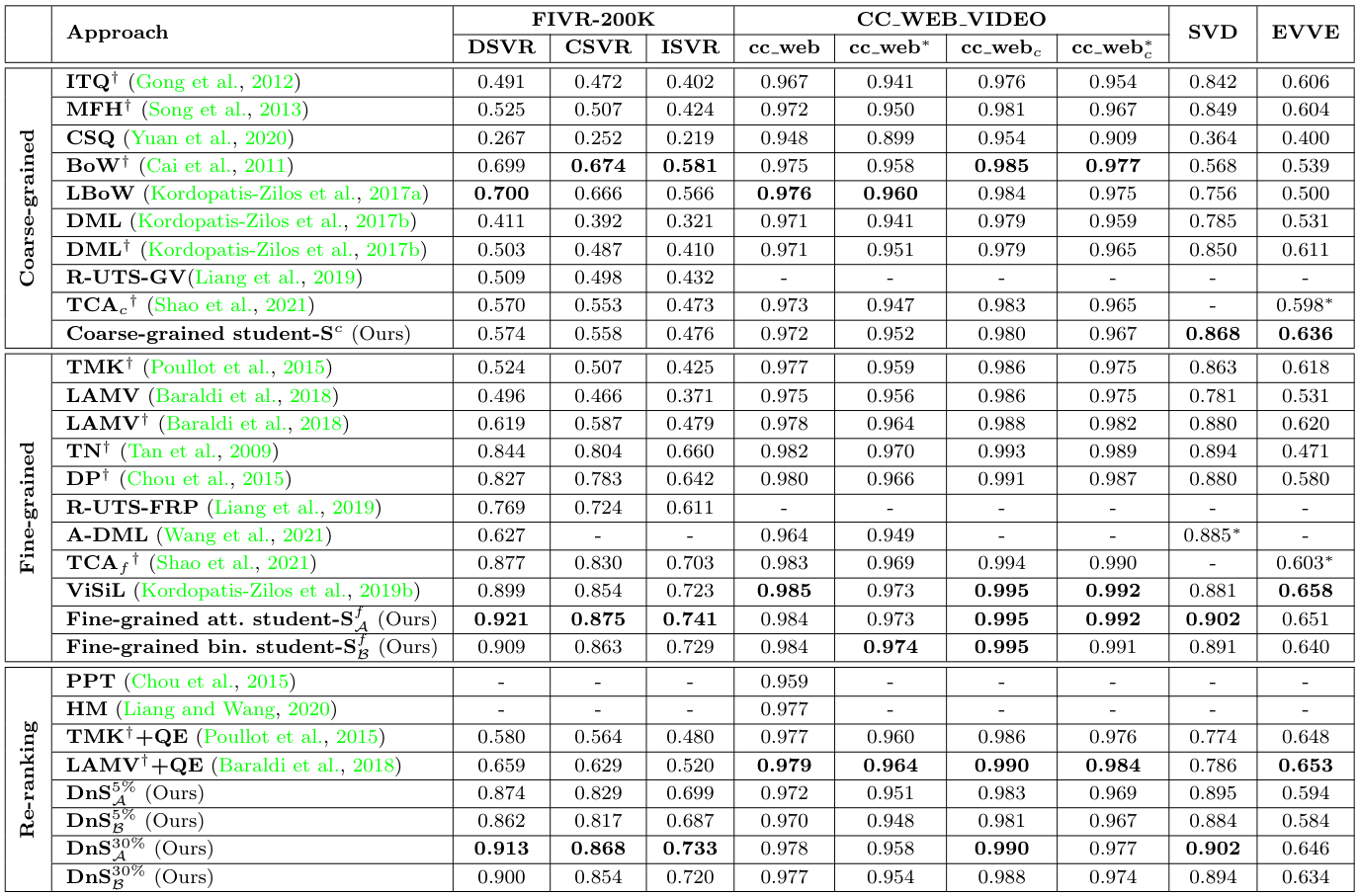
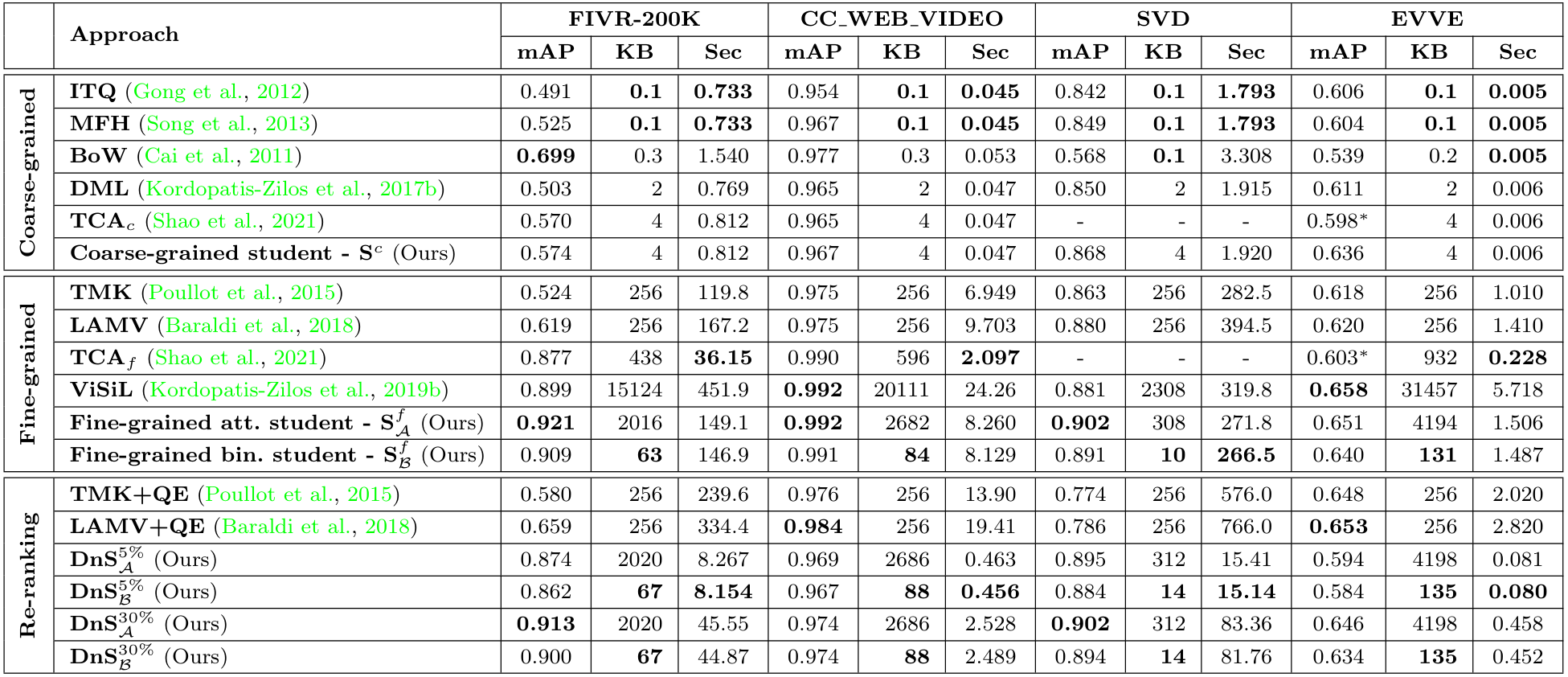
저자들은 여러 SOTA 모델들과 FIVR-200K, CC_WEB_VIDEO, SVD, EVVE 데이터셋에서 비교를 수행하였다. 지표는 mAP, 영상 서술자의 용량, 쿼리 당 검색 시간을 비교하였다.
모든 DnS 모델의 Teacher로는 $S^{f(2)}_\mathcal{A}$이 사용되었으며, 입력 데이터 중 5%, 혹은 30%의 데이터를 fine-grained student에게 보내 재분석하도록 하였다.
비교 결과, $S^f_\mathcal{A}$가 FIVR-200K, CC_WEB의 cleaned 버전, SVD에서 Video Retrieval 모델 중 가장 높은 mAP로 SOTA를 달성하였다.
DnS 모델들은 이 논문에서 제안한 $S^f$를 제외한 모델들 중 가장 높은 mAP를 달성하였으며, 검색 속도는 frame-level 방법 중에는 가장 낮은 수준으로 나왔다. 그러나 여전히 video-level 방법에 비해서는 매우 많은 시간이 소모되는 모습을 보여 아쉽다.
이 논문에서는 기존 Video Retrieval의 검색 속도 - 정확도 tradeoff를 해결하기 위해 다음과 같은 방법을 활용한다.
- Knowledge Distillation을 이용해, 정확하면서 속도는 teacher 모델보다 빠른 student model 학습 (Distill)
- 속도가 빠르지만 상대적으로 부정확한 coarse-grained student로 먼저 예측하고, 필요에 따라 느리지만 정확한 fine-grained student로 예측하도록 하는 selector network 학습 (Select)
Student의 경우에도, 단순히 fine-grained / coarse-grained만 설계한 것이 아니라, 저장공간을 아낄 수 있는 이진화 모델을 설계하거나, fine-grained model의 어텐션을 개선하고, coarse-grained의 경우 TCA와 NetVLAD를 적용하는 등 다양한 개선을 시도하였다.
이를 통해 일반적으로 쿼리 당 수백초의 검색 시간이 요구되는 frame-level 방법론들 보다는 빠른 8초대, 45초대의 검색속도를 가질 수 있었으나, 여전히 1초 미만의 검색 속도를 갖는 video-level 검색 방법들에 비해서는 많이 느린 상황이다.
그러나 distillation을 통해 모델의 정확도가 상당히 향상되어, 이 점도 주목할 만하다고 생각하며, video-level, frame-level 모두 검색 속도가 더욱 발전되었을 때 유사한 방식의 re-ranking 모델이 사용된다면 실용적이리라 생각된다.
저널 논문은 처음 읽어봐서 긴 논문에 꽤 놀랐는데, 읽는 데는 오래 걸려도 설명이 상세하여 좋았던 것 같다.