Convexity와 딥러닝 (Convex Function과 Convex Set)
딥러닝을 공부하다 보면, Convex 한 함수, 문제의 Convexity 등에 대한 언급을 자주 접하게 된다. 요즘은 국내에도 이를 다룬 쉬운 글이 많지만, 이상하리만치 필자는 이 Convexity를 이해하기가 힘들었다. 몇 시간에 걸친 공부를 마치고 이를 정리해보고자 한다.
Convex의 정의
Convex는 볼록하다는 것을 의미한다. 수학에서 Convex는 대상이 집합이냐 함수냐에 따라 개념이 약간 다른데, 먼저 함수에서의 Convexity를 알아보고, 집합에서의 Convexity를 간단히 알아본 후, 딥러닝과 Convexity의 상관관계에 대해 다루도록 하겠다.
함수의 Convexity
Convex 함수는 볼록 함수라고 하며, 이름 그대로 볼록한 함수를 의미한다. 이때, 우리가 고등학교에서 흔히 배운 것과는 달리 아래로 볼록한 것만 Convex라 하며, 위로 볼록한 함수는 Concave라 한다.

우리가 가장 잘 아는 Convex 함수는 위와 같은 이차함수이다. 이름 그대로 아래로 볼록한 모양의 그래프를 갖는다.
그렇다면 이러한 Convex 함수를 수학적으로 판단하는 방법은 무엇일까? 함수 위의 임의의 두 점을 연결하는 선을 그래프에 그었을 때, 그 선이 아래 그림과 같이 함수 그래프의 위쪽만을 지나가면 이 함수는 convex 한 함수이다.
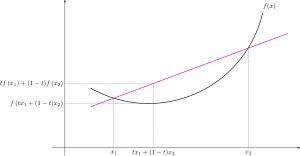
반면, 함수위의 임의의 두 점을 연결하는 선이 함수의 아래를 지난다면 이것은 non-convex 함수이다.
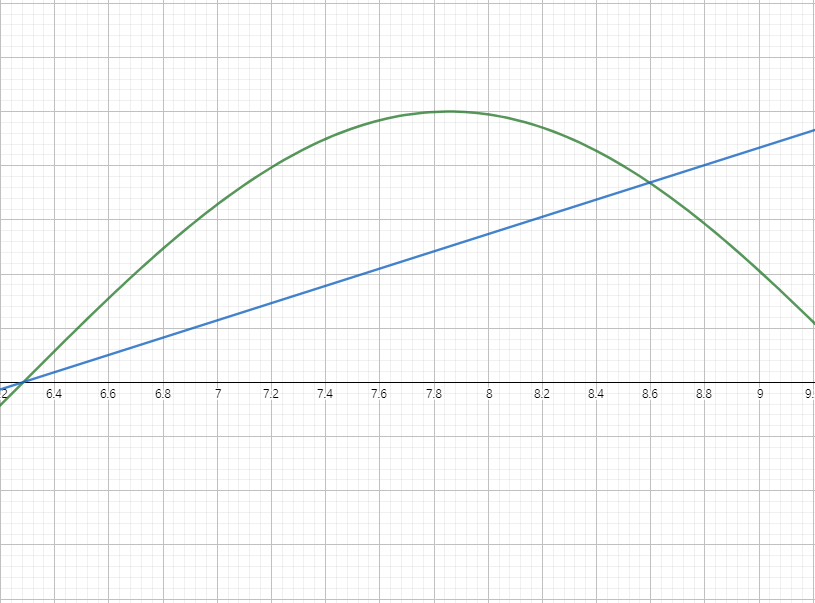
Convex 함수의 판별
함수 위의 임의의 두 점 $x,y$와 $[0,1]$ 사이의 값 $t$에 대해 다음이 식이 항상 성립하면 이 함수는 Convex 하다고 말할 수 있다.
$f(tx + (1-t)y) \leq tf(x) + (1-t)f(y)$
집합의 Convexity
구글에 Convex를 검색해보면 많은 글들이 집합의 Convexity를 다루고 있다. 이로 인해 내가 딥러닝에서의 Convexity를 이해하는데 조금 혼란이 있었던 것 같다.
Convex 한 집합을 볼록집합Convex Set이라고 부른다. Convex 집합은 집합이 이루는 공간 내의 두 점을 연결한 선분이 그 집합 안에 포함되는지, 포함되지 않는지에 따라 Convexity가 갈린다.
쉬운 이해를 위해 아래 예시들을 보자.


아래의 경우, 임의의 두 점 x와 y를 잇는 선분이 set의 바깥에 나와있어 Convex 하지 않다고 할 수 있다.
분리 초평면 정리Hyperplane separation theorem
Convex set에서 중요하게 알아두어야 할 것은 분리 초평면 정리이다. 두 개의 겹치지 않는(disjoint) 닫힌 유계 convex 집합 $A,B$을 분리해주는 초평면Hyperplane이 존재한다는 것이다.

Convexity와 딥러닝
이제 마침내 Convexity와 딥러닝이 갖는 상관관계이다. 딥러닝은 매우 복잡한 다변수 함수의 최적해를 경사 하강법을 통해 찾는 것이라고 지난 글에서 다뤘다.
경사 하강법을 사용할 때, convex 함수와 non-convex 함수에서 탐색한 해는 큰 차이를 갖는다.
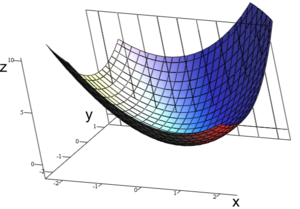
위와 같은 convex 함수의 경우, 우리가 딥러닝에서 경사 하강법을 통해 찾는 최저점이 단 하나 존재한다. 이 점을 전역 최적해Global Minimum이라고 한다.
Convex 함수에 대한 경사 하강법은 하나의 최고의 해로 수렴한다. 그러나 non-convex 함수에서는 그렇지 않다.

non-convex 함수는 무한히 넓은 함수 공간에서 여러 곳의 지역 최저점Local minima을 갖는다.
위 함수에서 이로 인하여, 경사 하강법을 시작하는 위치에 따라 서로 다른 최저점을 향해 결과가 수렴하게 된다. 예를 들어, 위 함수에서 1.5에서 경사 하강법을 시행하면 0.3 부근의 지역 최저점으로 수렴할 것이다. 그러나 2.5 부근에서 경사 하강법을 시행했다면, 조금 더 나은 결과를 갖는 5 부근의 지역 최저점으로 수렴할 것이다.
non-convex 함수의 문제는 우리가 어디가 전역 최적해인지를 알 수가 없다는 것이다. 이로 인해 non-convex 한 문제를 딥러닝으로 해결하려고 하면 학습이 잘 되지 않고 좋지 않은 지역 최저점에 갇히는 등의 문제가 발생한다.
이를 보완하기 위해 AdaGrad, RMSprop 등 다양한 Optimizer들이 연구되었다. 이들은 더 나은 지역 최저점을 찾기 위해 보완된 경사 하강법들로, 다음에 비교해보도록 하겠다.
Convex Set과 딥러닝
Convex Set들을 분리할 수 있는 초평면이 존재한다는 분리 초평면 정리를 기억하는가? 이에 따르면 닫힌 유계(경계가 존재하는 유한한) 집합을 구분할 수 있는 초평면이 존재한다. 문제는 이 초평면이 굉장히 찾기 어렵다는 것이다. 퍼셉트론이 사실 선형 분리기라는 것도 기억할 것이다. 퍼셉트론과 SVM을 비롯하여 머신러닝은 Convex 한 집합을 올바르게 분리하는 초평면을 찾는 수학적 모델이다.
이때 심층 신경망, 딥러닝이 갖는 강점이 나타난다. 심층 신경망의 층을 한 계층씩 늘릴 때마다, 신경망이 표현 가능한 데이터의 축이 하나씩 추가되는 효과를 갖는다. 이때, 고차원 공간의 데이터 포인트는 저차원 공간에 비해 선형 분리 가능한 축의 수가 많아져서, 선형 분리가 가능할 확률이 높아진다.
즉, 신경망의 계층이 쌓일수록, 분리하기 어려워 보이는 집합을 분리하는 초평면에 가까이 갈 수 있는 것이다.
Reference
Convex Functions, Convex Sets - ratsgo(이기창)님 블로그
Convex function, Hyperplane separation theorem - Wikipedia
CNN의 발전과 활용, 왜 딥러닝인가? (딥러닝의 강점 참조) - NYU Deep Learning
Special thanks to Keras Korea