경사하강법과 손실 함수: 심층 신경망 학습시키기 (Gradient Descent and Loss Function)
이 글은 나만 알기 아까운 딥러닝 시리즈에 포함된 글입니다. 그러나 전체 글을 읽지 않아도 이해할 수 있습니다. 전체 목차는 여기에서 확인하실 수 있습니다.
지난 글에서는 퍼셉트론이라는 모델을 활용해 간단한 문제를 해결하고, 퍼셉트론을 여러 계층으로 쌓아 복잡한 문제를 해결할 수 있는 방법을 배웠다. 그러나 다층 퍼셉트론(Multi-layer Perceptron)의 문제는 퍼셉트론의 개수가 늘어날 때마다, 개발자가 설정해야 할 가중치(Weight)가 많아져, 금방 사람의 직관으로는 설정이 불가능한 지점에 도달하는 것이었다.
예를 들어보자.
3과 4가 주어졌을 때, 7을 출력하는 퍼셉트론을 설계하는 것은 쉽다. 각 가중치가 1이고, 입력된 값과 가중치를 그대로 더해 출력하는 퍼셉트론을 쓰면 된다. 그러나, 784개의 입력을 받아 10개 중 하나의 값을 출력하는 다층 퍼셉트론을 설계하는 것도 이처럼 간단할까?
무엇보다 컴퓨터는 사람처럼 직관을 가지고 숫자를 떠올리지 못한다. 우리가 컴퓨터에게 올바른 숫자를 찾을 방법을 알려줘야 한다. 이때, 컴퓨터가 심층 신경망에서 올바른 매개변수를 찾을 수 있는 방법이 경사 하강법(Gradient Descent)이다.
손실 함수: 정답을 채점해주는 함수
경사 하강법을 배우기 전에 손실 함수(Loss Function) 얘기를 먼저 하고자 한다. 손실 함수란, 그 이름처럼 컴퓨터가 출력한 예측값이 우리가 의도한 정답과 얼마나 틀렸는지를 채점하는 함수이다.
가장 대표적인 손실 함수로 평균 제곱 오차(Mean Squared Error:MSE)가 있다.
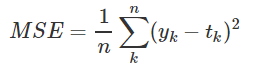
우리가 어떤 값을 신경망에 입력했을 때, 의도한 결과가 y=(1,2,3) 이라고 생각해보자. 그런데 랜덤으로 초기화된 변수를 가진 신경망은 멋대로 t=(3,2,1)이라는 출력 값을 내놨다.
신경망은 3개의 출력값 중 운 좋게도 하나의 값을 맞췄지만, 나머지 두 개의 값은 각각 1의 차이로 틀려버렸다. 이제 의도한 결과 y와 예측값 t를 이용해 위 평균 제곱 오차를 구해보면 아래와 같다.
MSE = {(1-3)^2 + (2-2)^2 + (3-1)^2} * 1/3 = 0.666...
만약 예측값이 (3,2,1)이 아니라 (4,5,6)이었다면 어땠을까? 계산해 보면 알겠지만 더욱 큰 에러 값이 나올 것이다. 예측값이 정답인 (1,2,3)이었다면? 혹은 정답에 아주 근사한 (0.9, 2.1, 2.999..)였다면?
손실 함수는 함수에 따라 차이는 있지만, 예측값이 정답에 가까울수록 0에 수렴하고, 정답과 거리가 멀 수록 큰 값을 출력한다.
이제 이를 어떻게 신경망의 가중치를 조절하는 데 사용할 수 있는지 알아보자.
경사 하강법: 방정식의 근사해 탐색 알고리즘
위에 적어놓은 경사 하강법의 소개를 보고 조금 긴장했을지도 모르겠다. 그러나 걱정할 필요 없다. 경사 하강법은 n차 함수의 근사해를 탐색하는 가장 쉽고 효과적인 방법 중 하나이다. 근사해란, 함수의 출력을 0에 가깝게(근사하게) 만드는 입력을 말한다.
일단 문제를 재정의해보자. 우리는 지금 모종의 문제를 해결하기 위해 신경망을 훈련시켜야 한다. 이 신경망은 x 데이터를 입력하면 우리가 원하는 y를 출력해야 하지만, 현재로서는 엉뚱한 예측값인 t를 출력한다. 우리는 이때, x와 y는 가만히 두고, 신경망의 가중치 w만을 수정해서 t가 y가 되도록 (적어도 y에 아주 가까운 값을 출력하도록) 만들어야 한다.
x와 x에 대한 y 값은 고정된 값이다. 예를 들어 y는 3이고 x는 1이라고 생각해보자. 우리의 신경망은 입력 x에 가중치 w를 곱하고 더하는 등의 연산을 한 결과를 출력한다. 간단히 wx라고 표현해보자. 이때, 우리는 1*w가 3이 되기를 바란다.
그러나, 랜덤으로 초기화된 w가 23이라면, 신경망은 엉뚱하게도 23을 출력할 것이다. 이 때, 손실 함수는 0과는 거리가 먼 값을 무언가 출력할 것이다. 컴퓨터는 이를 통해, 본인이 크게 틀렸음을 알 수 있다.
이제 컴퓨터는 가중치에 뭔가 수정을 가해서, 신경망을 고쳐야 한다. 손실(출력값)을 0으로 만드는 변수를 찾는 과정이라니 뭔가 떠오르지 않는가? 그렇다. 우리가 초등학교 때부터 학부 시절까지 계속 배운 방정식의 해를 찾는 과정이다!
신경망 내부의 변수(w)가 하나 늘어날 때마다 함수공간의 차원이 하나씩 증가한다. 또한, 각 퍼셉트론은 비선형 활성화 함수를 갖고 있기 때문에, 신경망의 함수 공간은 고차원의 울퉁불퉁한 그래프를 만든다. 이 함수에서 정확하게 손실을 0으로 만드는 가중치를 찾는 것은 불가능하기에, 신경망의 학습은 정확한 해가 아닌 근사해를 찾는 것을 목표로 한다.
예를 들어, 변수(신경망에서는 가중치)가 두 개인 함수는 아래와 같은 3차원 그래프를 만든다.

빨간색, 초록색 축은 각각 하나씩의 가중치이고, 파란색은 이에 따른 손실 함수의 값이다. 함수가 산맥같이 생긴 그래프를 만들고 있다. 저 그래프에서 가장 낮은 곳이 손실 값이 최소화되는, 가장 적절한 가중치를 갖는 포인트라고 볼 수 있다.
지역 최적해 탐색하기
이제 이론은 어느 정도 알았으니, 본격적으로 함수의 근사해를 찾아보자. 함수의 근사해에는 국소 최적해(Local minimum, 극솟값)와 전역 최적해(Global miminum, 최솟값)가 있다. 그 이름처럼 국소 최적해는 함수의 특정 구간에서의 최적의 해를 의미하고, 전역 최적해는 함수 전체에서 최고의 해를 의미한다. 함수 공간이 가중치의 범위에 따라 무한히 넓은 공간을 형성하기 때문에, 신경망과 같은 복잡한 문제의 근사해를 찾는 것은 기본적으로 국소 최적해를 찾는 것을 목표로 한다.

쉬운 설명을 위해 변수가 1개인 2차원 그래프에서 경사하강법을 통해 최적해를 찾아보고자 한다. 위 그래프에서, x=5일 때, 국소 최적해를 갖고, x=11일 때 전역 최적해를 갖는 것이 보일 것이다.
이 그래프를 만드는 함수를 f(x)라고 두고, 우리가 x의 초기값으로 랜덤하게 선택한 수, 7을 선택했다고 생각해보자.

x=7에서 그래프의 기울기는 위와 같이 나타난다. 그래프를 참고하여, 우리는 7과 가까운 지역 최적해가 x 축 위의 어느 방향에 있는지 알 수 있다.
이제 x를 해당 방향으로 옮겨주자.
x=7-(grad*lr)
7은 방금 x가 있었던 곳이고, grad는 7에서의 기울기다. lr은 learning rate(학습률)의 약자로 임의의 실수이다. 학습률을 크게 설정하면 x가 기울기 방향으로 크게 이동할 것이고, 작게 잡으면 조금씩 이동하며 적절한 값을 신중히 탐색할 것이다.

x가 7에서 지역 최적해가 있는 방향으로 이동했다. 이를 계속 반복하다보면 어떻게 될까?
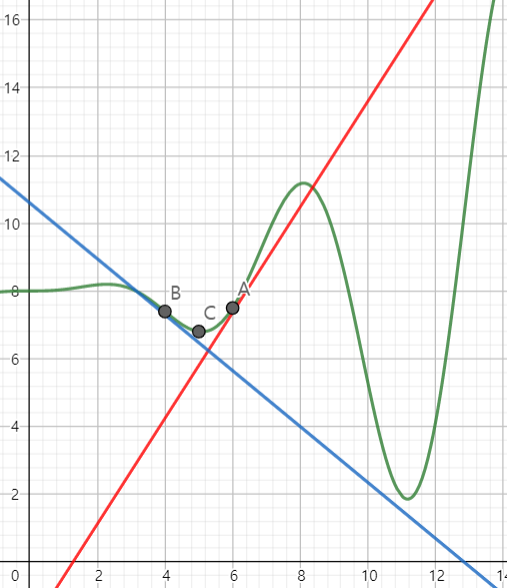
A에서 계속 좌측으로 이동하던 x는 B 지점에서 기울기가 바뀜에 따라 우측으로 이동할 것이다. 이를 반복하면서 변수는 결국 지역 최적해인 C에 수렴하게 된다.
고차원에서의 기울기
위에서 경사 하강법으로 변수가 하나인 함수의 근사해를 탐색해봤다. 그렇다면 변수가 여러 개인 고차원에서는 어떨까?
고차원에서의 기울기 탐색도 그렇게 어렵지 않다. 경사하강법을 위해 특정 변수에서의 기울기를 구해야 하는데, 이때 각 변수를 독립적으로 미분하는 편미분을 수행한다. 그 결과로, 기울기는 변수의 개수만큼의 원소를 가지는 벡터 형태로 나타난다.
예를 들어, 아래의 식에서 기울기를 구해보자.
f(x, y) = 2x^2+3y
y는 무시하고 x만을 편미분 하면, x의 기울기는 4x임을 알 수 있다. y도 같은 방법으로 미분하면 3을 기울기로 갖는다.
x=1, y=9일 때, 함수의 기울기는 (4,3)의 벡터로 나타난다.
(1,9) 입력에 (4,3) 기울기에 학습률 -0.1을 곱해 더해보자.
(0.6, 8.7)이 나온다. 이를 f에 넣고 같은 작업을 반복하다 보면, f의 값이 0에 가까워지는 근사해를 찾을 수 있다.
결론
이 글에서는 우선, 경사하강법을 위해 신경망의 결과가 얼마나 틀렸는지를 알려주는 손실 함수의 역할과 대표적인 손실 함수인 평균 제곱 오차를 알아봤다.
여러 가지 상황에 따라 활용 가능한 다른 손실 함수들의 소개를 다른 글에서 자세히 다뤄보고자 한다.
또한, 복잡한 신경망에서도 수천 개의 가중치를 조절해 최적의 결과를 내도록 신경망을 학습시킬 수 있는 경사 하강법을 소개했다. 그러나 경사 하강법에서 사용되는 편미분은 상당히 컴퓨팅 자원이 많이 필요하고, 일반적인 경사 하강법은 가장 가까운 지역 최적해를 탐색하기 때문에, 때로는 별로 좋지 않은 지역 최적해로 수렴하는 단점이 있다.

이를 해결하기 위해 rmsprop이나 Adagrad와 같은 변형된 경사하강법이 많이 등장하였는데, 이들의 소개와 비교는 다른 글에서 해보고자 한다.
다음에는 지역 최적해를 더욱 낮은 사양으로 찾을 수 있게 해주는 오차 역전파법에 대해 소개하고자 한다.
'강의 > 딥러닝 기초' 카테고리의 다른 글
| 데이터 일반화 vs 표준화 (Normalization and Standardization of Data) (3) | 2020.04.28 |
|---|---|
| Convexity와 딥러닝 (Convex Function과 Convex Set) (1) | 2020.04.13 |
| 퍼셉트론(Perceptron): 덧셈과 곱셈으로 뉴런 구현하기 (3) | 2020.01.06 |
| 왜 지금인가? - 딥러닝의 역사 (0) | 2020.01.06 |
| 나만 알기 아까운 딥러닝 연재 계획 (0) | 2020.01.05 |
댓글
이 글 공유하기
다른 글
-
데이터 일반화 vs 표준화 (Normalization and Standardization of Data)
데이터 일반화 vs 표준화 (Normalization and Standardization of Data)
2020.04.28 -
Convexity와 딥러닝 (Convex Function과 Convex Set)
Convexity와 딥러닝 (Convex Function과 Convex Set)
2020.04.13 -
퍼셉트론(Perceptron): 덧셈과 곱셈으로 뉴런 구현하기
퍼셉트론(Perceptron): 덧셈과 곱셈으로 뉴런 구현하기
2020.01.06 -
왜 지금인가? - 딥러닝의 역사
왜 지금인가? - 딥러닝의 역사
2020.01.06