9. 그래프 이론과 P-NP 문제 (Graph Theory and P-NP Problem)
어떤 그래프 $G$는 교점node(혹은 꼭짓점vertex)의 집합 $V$와 간선edge의 집합 $E$로 정의된다.
주로, 수학계에서는 꼭짓점, 컴퓨터 공학계에서는 노드(교점)이라는 표현을 사용한다.
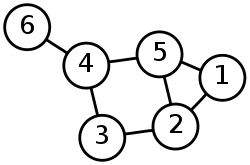
위 그래프는 다음과 같은 $V$와 $E$의 집합으로 나타내어 진다.
$$ V = \{1,2,3,4,5,6\}\\
E = \{(1,2), (1,5), (2,3), (2,5), (3,4), (4,5), (4, 6)\}$$
정의
- $(a,b)\in E$라면, 노드 $a$와 $b$는 인접adjacent해있다.
- 어떤 노드 $n$에 연결된 간선의 갯수를 노드의 차수degree라고 한다.
- 그래프에 루프loop나 다중 간선multiple edge이 없으면, 그 그래프는 단순simple하다고 한다. 반대의 경우는 복잡complex하다고 한다.
- 루프는 $(a,a)$와 같은 간선을 말한다.
- 다중 간선은 $(a,b), (b,a)\in E$와 같이 같은 노드들을 연결하는 간선이 여러 개인 경우를 말한다.
예제) 성별에 따른 연애 횟수
그래프를 응용할 수 있는 간단한 예제를 만들어보자.
$(f)$는 한 여성이 평생 사귄 남자친구의 수의 평균이라고 하자.
$(m)$은 한 남성이 평생 사귄 여자친구의 수의 평균이라고 하자.
우리가 우리나라의 모든 남녀에게 평생 사귄 연인의 수를 물어볼 수 있지 않은 한, 이를 알 방법은 없다. 그러나 $(f)$와 $(m)$ 중, 어떤 값이 큰지는 그래프를 이용해 알 수 있다.
아래와 같은 그래프를 생각해보자.

왼쪽의 노드들이 우리나라의 남자들, 오른쪽의 노드들이 우리나라의 여자들이고, 각 간선이 서로가 사귄 경험을 나타낸다고 보자. 2020년 8월 기준으로 그래프는 다음 수치를 갖는다.
$$ |V_m| = 25,851,388\\
|V_f| = 25,988,565\\
|E| = (\text{Total number of boy (girl) friends for all female (male). unknown})$$
$(f)$를 $(m)$으로 나누었을 때, 이 값이 1보다 크다면 $(f)$가 더 크고, 1보다 작다면 $(m)$이 $(f)$보다 큼을 알 수 있다.
$$ \frac{(f)}{(m)} = \frac{\frac{|E|}{|V_f|}}{\frac{|E|}{|V_m|}} = \frac{V_m}{V_f} = \frac{25,851,388}{25,988,565} \approx 0.995 \approx 1 $$
계산 결과, 여성과 남성은 평균적으로 비슷한 횟수의 연애 경험을 갖는다.
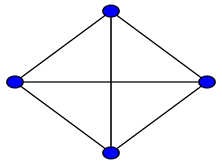
완전 그래프Complete Graph
모든 노드 사이에 정점이 존재하는 그래프를 완전 그래프라 한다.
$K_n$이 $n$개의 노드를 갖는 완전 그래프라면, $K_n$의 노드의 차수는 모두 $n-1$이 된다.
이분 그래프Bipartite Graph
어떤 그래프 $G=\{V, E\}$의 $V$를 $V_1, V_2$로 나누었을 때, $V_1$과 $V_2$사이의 간선만 존재하면 ($V_1$ 안의 노드간에는 연결이 없고, 오롯이 $V_1$과 $V_2$ 사이에만 연결이 존재) 이분 그래프라 한다.
특히, $V_1$의 원소와 $V_2$의 원소 사이에 모두 간선이 존재할 경우, 완전 이분 그래프라 한다.

그래프 색칠Graph Coloring 문제
간단한 예제 문제를 통해 그래프 색칠 문제를 배워보자.
한 대학에서 과목 $s_1,s_2, \cdots, s_5$의 시험을 본다고 하자. 아래 그래프에서, $s_a$와 $s_b$ 사이의 간선은 두 수업을 동시에 수강하고 있는 학생이 있음을 나타낸다.
즉, 서로 인접한 수업은 같은 시간에 시험을 봐서는 안된다. 또한, 시험 기간은 한정되어있기 때문에, 가능한 적은 시간안에 시험을 진행해야 한다.
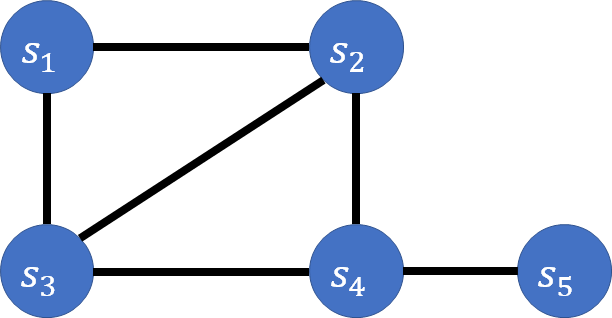
인접한 노드에 같은 시간을 할당하면 안되며 가능한 적은 시간을 써야 하는 문제, 이를 색깔로 바꿔 표현한 것이 그래프 색칠 문제이다.
즉, 어떤 그래프를 $G$개의 색으로 칠하는데, 가능한 최소한의 색 $\chi (G)$를 이용해 색칠하는 방법을 구하는 것이다.
이 문제는 대표적인 NP 완전 문제이다. 보통 P 문제는 컴퓨터에게 쉽다고 하고, NP 완전 문제는 컴퓨터에게 어려운 문제로 본다.
이 문제를 잘 해결하지 못할 경우, 필자처럼 중간고사를 3주간 치르게 된다.
그래프 색칠 문제의 풀이
어떤 그래프 $G={V,E}$에 대한 그래프 색칠 문제는 다음과 같이 풀 수 있다.
- 노드를 임의의 순서로 정렬한다. ($v_1, v_2, \cdots $)
- 색깔도 임의의 순서로 정렬한다. ($c_1, c_2, \cdots $)
- $v_i$를 $v_i$와 인접한 노드가 사용 중인 색을 제외하고 가장 낮은 순서의 색으로 칠한다.
만약 그래프의 노드의 차수가 최대 $d$라면, 알고리즘은 최대 $d+1$개의 색깔을 필요로 한다.
증명
$P(n)$이 $n$개의 노드를 가지고, 노드의 최대 차수가 $d$인 그래프 $G$를 최대 $d+1$개의 색으로 칠할 수 있다. 라고 보자.
$P(0)$은 당연히 맞다. 노드가 0개면 색 1개로 칠할 수 있다.
$P(n+1)$은 $n+1$개의 노드가 있는 그래프이다. 해당 그래프에서 가장 많은 간선 $d$개를 갖는 노드 $v_{n+1}$을 빼고 생각해보자.
$P(n)$이 참이므로 색칠 가능하다. 이제 빼놓았던 노드 $v_{n+1}$을 다시 넣자.
$v_{n+1}$이 간선 $d$개를 통해 연결된 노드와 다른 색 $C_{d+1}$로 칠해질 것이다.
P-NP 문제
답이 yes or no (혹은 True or False)로 반환되는 문제를 결정 문제Decision Problem라고 한다. 그래프 색칠 문제의 경우, 임의의 그래프를 $n$개의 색으로 조건에 맞게 칠할 수 있는가?가 결정 문제에 해당한다.
결정 문제는 P 문제와 NP 문제로 나뉜다.
P 문제는 다항식 시간Polynomial Time(선형 시간) 안에 True or False의 결론을 낼 수 있는 결정 문제를 말한다.
NP 문제는 비결정적 알고리즘Non-deterministic Polynomial을 이용하여 다항식 시간 안에 해결 가능한 문제를 말한다.
P 문제는 직관적으로 이해하기 쉬운데 반해, NP 문제는 헷갈릴 것이다. 예시를 들어보자.
$$A=\{2,5,1,-12,-7, 6\}$$
위 집합 $A$가 주어졌을 때, $A$의 부분집합 중에서 합이 $0$이 되는 부분집합이 있는가? 라는 결정 문제가 있다고 보자.
일반적인 방법으로, 이에 대답하려면하려면 합이 $0$인 부분 집합이 나올 때까지 가능한 모든 부분 집합을 조합해보아야 한다. $n$개의 원소로 조합할 수 있는 부분 집합의 수는 $\sum_{k=1}^n nCk$로 선형 시간을 초과한다.
그러나 누군가 우리에게 $A$의 부분집합 중 $\{-7, 6, 1\}$이 있다는 힌트를 제공해준다면, 우리는 이 부분집합이 정말로 있는지만 $A$ 안에서 조사해보면 된다. 즉, NP 문제는 검산이 다항식 시간 안에 가능하다.
눈치가 빠르다면, P 문제는 모두 NP 문제이기도 함을 눈치챘을 것이다. ($P\in NP$)
P 문제 역시, 해답이 주어지면 다항식 시간 안에 검산이 가능하기 때문이다.
반면, $NP\in P$는 증명되지 않았는데, 이는 100만 달러의 상금이 걸린 밀레니엄 문제 중에 하나이다.
만약 $NP\in P$가 참이라면, 이 세상의 모든 문제는 다항식 시간안에 풀 수 있는 문제로 환원되며, 이는 곧 컴퓨팅 가능해진다는 것을 의미한다.
환원reduction
문제 $A,B$의 난이도를 비교하는 방법으로 환원이 사용된다.
문제 $A$가 "어떤 집합을 정렬하는 문제"이고, $B$가 "어떤 집합의 중앙값을 찾는 문제"라 하자.
문제 $A$를 풀 수 있다면 당연히 문제 $B$도 풀 수 있다. 중앙값을 찾기 위해선 집합을 정렬해야하기 때문이다.
그러므로, 문제 $B$는 $A$보다 쉽다고 할 수 있고, $B$는 $A$로 환원된다고 표현한다.
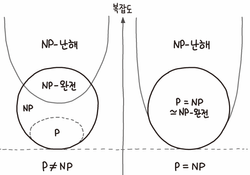
NP-완전, NP-난해 문제
모든 NP 문제를 다항 시간 내에 어떤 문제 $A$로 환원할 수 있다면, 그 문제 $A$를 NP-난해NP-Hard 문제라고 한다.
만약 이때, 환원된 $A$가 여전히 NP 문제라면, 그 문제는 NP-완전NP-Complete 문제가 된다.
$P=NP$인지 $P\neq NP$인지가 밝혀지지 않아 정확하지는 않지만 P 문제와 NP 문제의 관계도는 다음과 같다.
'학부 수업 > 이산수학' 카테고리의 다른 글
| 11. 그래프 이론과 신장 트리 (Spanning Tree) (1) | 2020.12.05 |
|---|---|
| 10. 매칭 알고리즘 (Matching Algorithm) (1) | 2020.10.18 |
| 8. RSA 암호화 (RSA Encryption Algorithm) (1) | 2020.10.17 |
| 7. 정수론: 오일러의 피 함수과 페르마의 소정리 (Number Theory: Euler's Phi Function and Fermat's Little Theorem) (2) | 2020.10.17 |
| 6. 정수론: 암호화, 복호화 (Number Theory: Encryption and Decryption) (2) | 2020.10.17 |
댓글
이 글 공유하기
다른 글
-
11. 그래프 이론과 신장 트리 (Spanning Tree)
11. 그래프 이론과 신장 트리 (Spanning Tree)
2020.12.05 -
10. 매칭 알고리즘 (Matching Algorithm)
10. 매칭 알고리즘 (Matching Algorithm)
2020.10.18 -
8. RSA 암호화 (RSA Encryption Algorithm)
8. RSA 암호화 (RSA Encryption Algorithm)
2020.10.17 -
7. 정수론: 오일러의 피 함수과 페르마의 소정리 (Number Theory: Euler's Phi Function and Fermat's Little Theorem)
7. 정수론: 오일러의 피 함수과 페르마의 소정리 (Number Theory: Euler's Phi Function and Fermat's Little Theorem)
2020.10.17