11. 그래프 이론과 신장 트리 (Spanning Tree)
보행walk이란 간선으로 연결된 노드들의 시퀀스이다. 예를들어, $v_1 - v_2 - v_3 - \cdot - v_k$는 $v_1$에서 시작하여 $v_k$로 가는 보행이다. 보행의 길이는 시작 노드부터 끝 노드까지 과정에 있는 노드의 갯수이다.
만약 보행에 포함된 노드가 모두 다른 노드일 경우, (즉, 한 번 방문한 노드는 재방문하지 않는 경우) 이는 경로path라고 한다.
- 만약 노드 $u$에서 $v$로 가는 보행이 존재한다면, $u$에서 $v$로 가는 경로 또한 존재한다.
- $u$에서 $v$로 가는 경로가 존재한다면, $u$와 $v$는 연결되었다connected고 한다.
- 그래프의 모든 노드가 서로 연결되었다면, 연결 그래프connected graph라 한다.
어떤 보행의 시작 노드와 끝 노드가 같다면, 이 보행은 닫힌 보행closed walk이라 한다. 이때, 보행에 속한 노드가 3개 이상이고, 이 보행의 끝 노드를 제외한 모든 노드가 다른 노드라면 순환cycle이라고 한다.
- 닫힌 보행: $a - b - c - b - a, a - a$
- 순환: $a - b - c - d- a$
트리tree
연결 그래프이면서, 순환이 없는acyclic 그래프는 트리tree라고 한다. 트리에서, 차수가 1인 노드를 리프leaf라고 한다.
트리의 부그래프 중에, 연결된 그래프들은 모두 트리이다. 이 부그래프들을 부트리subtree라 한다.
$n$개의 노드를 갖는 트리는 $n-1$개의 간선을 갖는다. 이는 귀납적으로 증명 가능한데, $E(n)$이 $n$개의 노드를 가진 트리의 간선 갯수일 때, $E(n+1) = E(n) + 1$이고, $E(2) = 1$이다.
신장 트리spanning tree:ST
신장 트리(스패닝 트리)는 어떤 연결 그래프 $G$의 모든 노드를 포함하며, 트리인 부그래프를 말한다.
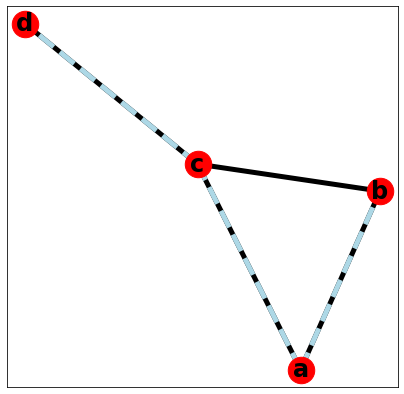
모든 연결 그래프는 신장 트리를 갖는다.
최소 신장 트리Minimum Spanning Tree
가중치가 있는 연결 그래프에서, 가중치의 합이 가장 적은 간선들로 구성된 스패닝 트리를 최소 신장 트리라고 한다.
최소 신장 트리를 얻기 위한 다양한 알고리즘이 존재한다.
크루스칼 알고리즘Kruskal Algorithm
탐욕법을 이용한 알고리즘이다. 매번 가능한 최선의 선택 즉, 가장 가중치가 낮은 간선을 선택하는데, 해당 간선을 선택하였을 때 트리에 순환이 발생하면 해당 간선은 포기한다. 이를 반복하여 전체 노드를 연결하면 최소 신장 트리가 된다.
귀납법을 통한 증명
$S$가 크루스칼 알고리즘으로 선택된 $n$번째까지의 간선들의 집합이라 하자. 크루스칼 알고리즘이 맞다면 아래가 성립한다.
$$ \exists \text{ MST } T = (V, E) \text{ for G such that } S \subseteq E $$
$P(n)$일 때, $S$는 비어있으므로 $S\subseteq E$는 참이다.
$e$가 알고리즘에 의해 $n+1$번째로 선택된 간선이라 하고, $T*$이 $S \subseteq E*$인 $(V, E*)$ MST라 하자.
$e\in E*$인 경우, $S\cup {e} \subseteq E*$이므로 참이다.
$e\not\in E*$인 경우, 알고리즘에 의해 $S\cup {e}$는 순환이 없으므로, $(V, E* \cup e)$에 순환이 있는 건데, 알고리즘이 $e$를 선택한 것은 $E*$에 속한 $e$와 충돌하는 간선 $e'$보다 $e$의 가중치가 작거나 같기 때문이다. 그러므로 $e'$를 $e$로 대체할 경우, 새로운 트리 $T**$은 충돌 요소가 사라졌으므로 순환이 없고, 여전히 연결 그래프이며 $G$의 모든 노드를 포함한다.
그러므로 $T**$는 $G$의 스패닝 트리이며, $\{\text{weight}(e) \leq \text{weight}(e')$이고 $T*$가 MST이므로 $T**$도 최소 스패닝 트리이다.
'학부 수업 > 이산수학' 카테고리의 다른 글
| 13. 그래프 이론과 오일러 순회, 해밀턴 경로 (Euler Tour, Hamiltonian Path) (0) | 2020.12.06 |
|---|---|
| 12. 통신 네트워크 (Communication Networks) (0) | 2020.12.06 |
| 10. 매칭 알고리즘 (Matching Algorithm) (1) | 2020.10.18 |
| 9. 그래프 이론과 P-NP 문제 (Graph Theory and P-NP Problem) (2) | 2020.10.18 |
| 8. RSA 암호화 (RSA Encryption Algorithm) (1) | 2020.10.17 |
댓글
이 글 공유하기
다른 글
-
13. 그래프 이론과 오일러 순회, 해밀턴 경로 (Euler Tour, Hamiltonian Path)
13. 그래프 이론과 오일러 순회, 해밀턴 경로 (Euler Tour, Hamiltonian Path)
2020.12.06 -
12. 통신 네트워크 (Communication Networks)
12. 통신 네트워크 (Communication Networks)
2020.12.06 -
10. 매칭 알고리즘 (Matching Algorithm)
10. 매칭 알고리즘 (Matching Algorithm)
2020.10.18 -
9. 그래프 이론과 P-NP 문제 (Graph Theory and P-NP Problem)
9. 그래프 이론과 P-NP 문제 (Graph Theory and P-NP Problem)
2020.10.18