Camera 시스템
핀홀 카메라
사진을 촬영하기 위해 필름을 그대로 찍고자 하는 상에 노출시키면, 상의 여러 부분에서 반사되어 온 광선(Ray)들이 무분별하게 필름의 여러 영역에 도달하여 사진을 찍을 수 없다.
그래서 상의 한 점(영역)에 반사된 광선이 필름의 한 점에만 맺히도록 핀홀 카메라 모델이 고안되었다.
3차원의 세상에 존재하는 한 점 $P$의 이미지 상에서의 위치 $P'$는 어떻게 구할까?
3D 좌표 $P$에서 2D 좌표 $P'$로의 변환은 삼각형의 닮음을 이용하여 다음과 같이 수행된다.
핀홀을 원점 $O$로 두고, 핀홀에서 이미지 평면에 내린 수선의 발인 광학 축(optical axis)을 설정한다.
점 $P, O$ 그리고 광학 축이 이루는 직각 삼각형과 광학축, $O, P'$가 이루는 직각 삼각형의 닮음을 이용하여 $P'$를 구할 수 있다. 이때, 핀홀과 이미지 평면의 거리인 focal length $f$, 핀홀과 $P$가 위치한 광학 축의 좌표 $z$가 사용된다.
$$ P'^T = [fx / z, fy / z] $$
이 방법은 변수 $z$를 나눠서 사용하기 때문에 비효율적이고 비선형적이다.
$P'$ 변환을 선형적으로 수행하기 위해 동차(Homogenous) 개념이 도입된다.
동차 좌표계
3차원 좌표와 2차원 좌표간의좌표 간의 변환을 수행하는 대신, 3차원 좌표에 차원을 하나 추가하여 3차원 좌표 간의 변환을 수행한다.
$$ \begin{bmatrix} x\\ y \end{bmatrix} \rightarrow \begin{bmatrix} u\\ v\\ w \end{bmatrix} \rightarrow \begin{bmatrix} u/w\\ v/w \end{bmatrix}$$
어떤 직선을 나타내는 식 $ax + by +c = 0$을 $l = \begin{bmatrix} a \\ b \\ c \end{bmatrix}$로 나타낼 수 있는데, 이 직선 위에 점 $p=\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$가 존재함을 다음과 같이 나타낼 수 있다.
$$ l^Tp = ax+by+c = 0$$
동차 좌표를 이용하면 어떤 두 직선 $l, m$의 교점을 $l \times m$, 두 점 $p, q$를 지나는 직선을 $p \times q$로 나타낼 수도 있다.
특히, 어떤 두 직선의 교점을 외적으로 구하여 $[u, v, w]^T$가 나왔다고 할 때, $[u/w, v/w, 1]^T$가 두 직선의 교점이다.
그런데, 만약 $w=0$이라면, 교점이 point at infinity에 있다고 하며, 두 직선이 평행함을 의미한다.
동차 좌표를 이용하여 rigid body transform을 선형으로 다음과 같이 나타낼 수 있다.
$$ \begin{bmatrix} u' \\ v' \\ w' \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & t_x \\ r_{21} & r_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} u\\ v \\ w \end{bmatrix} $$
월드 좌표계의 점을 2D 좌표로 변환해 보자.
$$ \begin{bmatrix} f_x & 0 & 0 & 0 \\ 0 & f_y & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} f_xx \\ f_yy \\ z \end{bmatrix} \equiv \begin{bmatrix} f_xx/z \\ f_yy/z \\1 \end{bmatrix} $$
그런데 이때, 위 변환을 수행하면 변환된 2D 좌표가 이미지 평면과 광학 축의 교점을 원점으로 하게 된다.
그러나 픽셀 좌표계는 원칙적으로 이미지의 좌상단을 원점으로 하기 때문에, $p$를 추가하여 좌표의 변환을 수행해 준다.
$$ \begin{bmatrix} f_x & 0 & p_x & 0 \\ 0 & f_y & p_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} f_xx + zp_x \\ f_yy + zp_y \\ z \end{bmatrix} $$
카메라 모델
일반적으로 카메라를 다음과 같이 모델링한다.
월드 좌표계의 한 점 $X$를 $[R | t]$(Extrinsic Parameters)로 카메라 좌표계로 변환한 후, $K$(Intrinsic Parameter) 행렬을 통해 픽셀 좌표 $P$로 변환한다.
$$ P \equiv K[R|t]X $$
$$ K = \begin{bmatrix} f_x & 0 & p_x \\ 0 & f_y & p_y \\ 0 & 0 & 1 \end{bmatrix} $$
$$ [R|t] = \begin{bmatrix} r_{11} & r_{12} & t_x \\ r_{21} & r_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix} $$
이때 카메라의 내부적 요소 (렌즈, focal length 등)에 대한 행렬 $K$를 Intrinsic Parameters, 외부적 요소 (위치, 각도 등)에 대한 행렬 $[R|t]$를 Extrinsic Parameters라고 한다.
카메라의 Intrinsic / Extrinsic Parameter를 알아내는 과정을 카메라 캘리브레이션(Calibration)이라고 한다.
일반적으로 특정한 크기를 가진 2D 체크보드 판을 사용하여 수행하는데(Zhang's Method), 이때 intrinsic parameter는 고정된 반면, extrinsic parameter는 매 이미지마다 다르다.
핀홀의 크기와 렌즈
핀홀 카메라에서, 핀홀은 말 그대로 작아야 한 점에서 반사된 광선 중 일부만을 걸러내어 또렷한 이미지를 얻을 수 있다.
그러나 핀홀이 작으면, 센서로 전달되는 빛의 양이 적어져 이미지가 어두워지고, 그렇다고 크면 흐린 이미지를 얻게 된다.
한편, 핀홀이 마냥 작아져도 회절로 인하여 흐린 이미지를 얻게 되어, 핀홀 크기를 정하는데 문제가 있다.
그래서 카메라는 렌즈를 사용하는데, 이를 Thin Lens Model이라 한다.
Thin Lens Model
핀홀 카메라는 센서로 향하는 여러 광선(Ray)들을 막아 하나의 광선만이 센서의 한 점에 맺히게 한다.
한편 렌즈는 같은 곳에서 날아오는 광선들을 회절 시켜 한 점으로 모아 결과적으로 더 밝으면서도 또렷한 이미지를 얻게 해 준다.
이때, 렌즈의 중심점을 통과하는 광선은 회절 없이 직선으로 들어가게 된다.
한편, 광학 축과 평행하게 렌즈를 통과한 광선들은 렌즈 뒤의 한 점에서 교차하는데, 이 점을 focal point라고 한다.
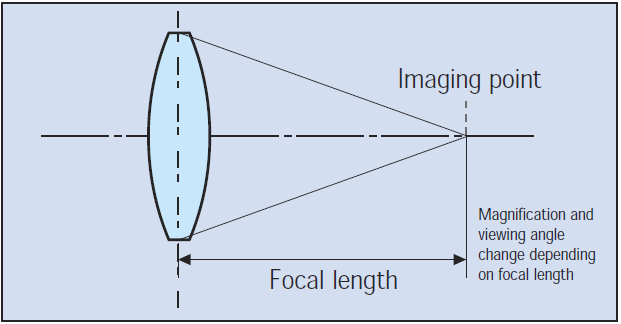
즉, thin lens model에서 focal length는 센서까지의 거리가 아니다.
Thin Lens Model의 문제는 이미지에 피사계 심도(Depth of Field)가 생기는 것이다.
카메라와 렌즈의 거리 $d$에 따라, 렌즈를 통과한 광선들이 모이는 지점이 변하기 때문에 초점이 잘 맞는 거리 구간이 생기게 된다.
카메라의 초점 거리를 조절하기 위해선, 렌즈와 물체의 거리 $D$, 렌즈와 센서의 거리 $D'$, 렌즈와 focal point의 거리 $f$ 중 하나를 바꿔야 한다.
$D, D'$는 고정되어 사실상 바꾸기 어려우므로(카메라를 찌그러뜨리거나 촬영 구도를 바꾸지 않는 이상), $f$를 바꿔야 하는데, 이는 조리개를 이용한다.
조리개를 통해 렌즈가 모으는 빛의 영역을 조절하면 $f$를 조절할 수 있다.
시야각 (Field of View)
카메라가 얼마나 더 많은 영역을 담을 수 있는지 평가하기 위해서는, 카메라의 화각을 사용해야 한다.
카메라로 촬영 가능한 물체의 크기는 원근법에 의해 얼마든지 변할 수 있기 때문이다.
카메라의 시야각 $\phi$는 카메라의 센서의 세로 크기 $d$와 focal length $f$에 의해 다음과 같이 정의된다.
$$ \phi = 2\tan^{-1}(\frac{d}{2f}) $$
시야각을 늘리기 위해서는 $f$를 줄여야 한다. (센서의 크기는 변경이 불가하니까...)이 또한 위처럼 조리개를 사용한다.
이미지 센서 for Color Image
컬러 이미지는 Red, Green, Blue의 3 채널로 구성된다.
이를 촬영하기 위해, 각 색상의 강도를 구해줘야 하는데, 이를 위해서 센서 3개가 필요하게 된다.
고급 카메라에서는 프리즘 빔 스플리터를 사용해 빛을 3 원색으로 쪼개어 각각의 센서로 보내지만, 이는 경제적으로 비용이 많이 들게 된다.
그래서 일반적으로 카메라는 하나의 센서에 베이어 필터라는 필터를 씌워 RGB 값을 얻는다.
$2\times 2$ 크기의 센서에 R, G, B 각각의 색만 투과하는 필터를 씌우고, 부족한 정보는 보간으로 채우는 것이다.
이때, 초록색 센서가 다른 색에 비해 많은 것을 알 수 있는데 이는 사람의 눈이 초록색에 더 민감하기 때문이라고 한다.
'Deep Learning > 영상처리' 카테고리의 다른 글
| 코너 검출 (Corner Detection) (0) | 2023.03.08 |
|---|---|
| Line Fitting (RANSAC, HOUGH transform) (0) | 2023.03.08 |
| 엣지와 그래디언트 (Edge and Gradient) (0) | 2023.03.07 |
| 이미지 필터링 (Image Filtering) (0) | 2023.03.07 |
| [Python/OpenCV] 투영을 이용한 이미지 변환 (0) | 2023.02.22 |