Line Fitting (RANSAC, HOUGH transform)
오늘은 이미지 안에 존재하는 어떤 형태, 특히 직선을 검출하는 방법들을 배워보자.
선행 지식으로 Edge Detection을 알아야 하니 혹시 모르시는 분들은 이전 글을 참고 바란다.
이미지 안의 형태를 검출하는 Model Fitting은 다음과 같은 요소들로 구성된다.
- Data: Fitting을 수행할 이미지의 정보, 여기선 Edge Detection 된 결과를 사용한다.
- Model: Fitting하여 찾아낼 형태 정보, 직선, 곡선, 도형 등이 될 수 있다.
- Objective Function: Fitting 결과를 평가하기 위한 함수이다.
Fitting이 진행되는 Edge Detection 결과 이미지는 다음과 같은 형태이다.

우리가 보기에야 선이나 곡선을 인지하는 것이 어렵지 않지만, 실제로는 다음과 같은 요소들이 Fitting을 방해한다.
- 너무 많은 Edge들: 우리가 찾고자 하는 직선 이외에도 수많은 Edge들이 검출되어 있다.
- Missing Points: 위 이미지에서도 알 수 있듯이, 직선 중간에 Edge 검출이 실패하여 잘려있거나 한 부분이 있다.
- Noise: 이미지나 detected edge의 노이즈로 인한 검출이 어려움이 있을 수 있다.
최소 제곱합 방법 (Least Squared Method)
직선의 방정식 $y_i = mx+b$를 이용한 간단한 방법이다.
우리가 알아내야 할 $m, b$값을 $w$ 벡터로 묶어 $Y = w^TX$로 표현해 보자.
위 식에서 $Y- w^TX = 0$가 유도되기 때문에, 미분을 통해 식이 성립되는 $w$를 구하면 된다.
$$ \sum^k_{i=1}(y_i - w^Tx_i)^2 \rightarrow ||Y-Xw||^2_2 $$
$$ w = (X^TX)^{-1}X^TY $$
$n$개의 파라미터를 갖는 $w$를 구하려고 할 때, $n$개의 독립된 $X, Y$ 데이터가 있으면 정확한 $w$값을 구할 수 있다.
한편, $n$개 미만의 독립된 $X,Y$ 데이터가 있으나, 전체 $X, Y$ 데이터의 수 $m$이 $n$보다 크다면 0에 가까운 $w$값 (근삿값)을 구할 수 있다.
만약 $m$이 $n$보다 적다면, 무한히 많은 $w$ 값들이 존재한다. (local minima)
RANSAC 방법 (RANdom SAmple Consensus)
위에서 배운 LS 방법은 outlier에 매우 취약한 특징이 있다.
outlier에 강건한 Line Fitting 방법으로 RANSAC이 있다.
Random Sample이라는 이름에서 알 수 있듯이, RANSAC은 전체 edge 데이터 중 일부를 샘플링하여 사용한다.
- 전체 점들 중 SUBSET_SIZE 개의 점을 랜덤으로 선택한다.
- 선택한 점으로 Least Squared 방법을 사용해 모델(직선)을 만든다.
- 만들어진 직선과 전체 점들의 거리를 구한다.
- 거리가 THRESHOLD 미만인 점들을 찾는다. (inlier)
- 1~4의 과정을 NUM_TRIAL 회 반복하여, 가장 많은 inlier가 있는 모델을 취한다.
RANSAC의 파라미터들은 다음 기준으로 고르면 된다.
- SUBSET_SIZE: 모델을 구성하는 변수의 개수 (e.g. 직선은 $y=mx+b$ 이므로 $m, b$ 2개이다.)
- THRESHOLD: 데이터의 scale 등을 고려하여 적당히 고른다.
- NUM_TRIAL: 확률적으로 최적의 모델을 고를 수 있는 횟수를 고려하여 정한다.
- $r$: fraction of outlier, 전체 데이터 중 outlier의 비율
- $s$: subset_size
- $N$: trial의 횟수
- $s$개의 점을 $N$회 뽑았는데, 전부 outlier가 섞인 뽑기일 확률은 대략 아래와 같다.
$(1-(1-r)^s)^N$ - 그렇다면 한 번이라도 inlier로만 구성된 뽑기를 할 확률은 다음과 같다.
$$ 1-(1-(1-r)^s)^N $$ - RANSAC이 성공할 확률 $C$는 다음과 같다.
$$ C\geq 1-(1-(1-r)^s)^N $$ - 그렇다면 실행 횟수 $N$은...
$$ N\geq \frac{\log(1-C)}{\log(1-(1-r)^s)} $$
RANSAC은 간단하고 효율적이면서도, 효과적이다. 그러나 설정해야 할 파라미터가 많고, 이론적이지 않고 경험적이며, 아웃라이어가 너무 많으면 실행을 아주 많이 해야 하여 좋지 않다.
허프 변환 (Hough Transform)
허프 변환은 투표 기반의 방식으로 여러 개의 선들을 한 번에 찾을 수 있으며, 노이즈에도 어느 정도 강인하다.
다만 파라미터가 늘어날 때마다 탐색해야 할 양이 기하급수적으로 증가하는 단점이 있다.
- 먼저 Parameter Space를 정의한다.
- Parameter Space는 직선을 구성하는 파라미터(e.g. $m, b$)로 구성된다.
- Image Space의 한 점 ($x,y$)은 Parameter Space의 직선($b = -xm + y$)이 된다.
- Parameter Spcae의 한 점은 Image Space의 직선($y = mx + b$)이 된다.
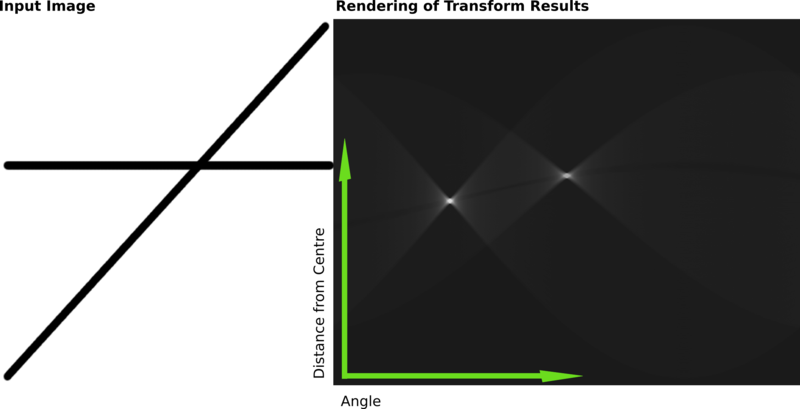
- 이 Parameter Space의 직선들의 교점이 바로 Image Space의 두 점이 이루는 직선이다.
- $m, b$는 무한대의 범위를 가지므로, 대신 직선의 각도 $\theta$와 직선의 길이 $p$를 사용한다.
- $\theta$는 0~180도, $p$는 이미지의 대각선 길이만큼의 최댓값으로 제한된다.
- Parameter Space를 일정 간격으로 나눈다. (이산화 한다.)
- 이미지의 edge point들을 Parameter Space로 이동시킨다.
- 이때, 이동된 Parameter Space의 직선이 지나는 곳마다 투표를 1씩 증가시킨다.
- 모든 edge들을 이동시키고 가장 표가 많은 영역들이 직선이 존재하는 영역이다.
'Deep Learning > 영상처리' 카테고리의 다른 글
| SIFT: Scale Invariant Feature Transform 을 이용한 Blob Detection (0) | 2023.03.08 |
|---|---|
| 코너 검출 (Corner Detection) (0) | 2023.03.08 |
| 엣지와 그래디언트 (Edge and Gradient) (0) | 2023.03.07 |
| 이미지 필터링 (Image Filtering) (0) | 2023.03.07 |
| Camera 시스템 (0) | 2023.03.06 |
댓글
이 글 공유하기
다른 글
-
SIFT: Scale Invariant Feature Transform 을 이용한 Blob Detection
SIFT: Scale Invariant Feature Transform 을 이용한 Blob Detection
2023.03.08 -
코너 검출 (Corner Detection)
코너 검출 (Corner Detection)
2023.03.08 -
엣지와 그래디언트 (Edge and Gradient)
엣지와 그래디언트 (Edge and Gradient)
2023.03.07 -
이미지 필터링 (Image Filtering)
이미지 필터링 (Image Filtering)
2023.03.07