2. 수학적 귀납법과 예제를 통한 증명 (Proof by Induction)
증명은 어떤 명제Proposition가 참 혹은 거짓임을 어떤 공리계Set of Axioms에 기반한 논리적 추론Logical Deductdion을 통해 보이는 것이다.
증명의 방법에는 크게 3가지가 있다.
- 직접 증명Direct Method
- 예제를 통한 증명by Contradiction
- $p$가 참이란 예제를 보이는 것
- $\neg p$가 거짓이란 예제를 보이는 것
- 귀납법을 통한 증명by Induction
"$p: \sqrt{2} $는 무리수이다" 예제로 증명하기
$\neg p: \sqrt{2} \text{ is rational.} $
$p$를 증명하기 위해, $\neg p$, "$\sqrt{2}$가 유리수이다"가 거짓임을 증명하면 된다.
$\sqrt{2} = \frac{a}{b} \text{(fractional number in lowest terms)}\\
2 = \frac{a^2}{b^2}\\
2b^2=a^2$
이때, $a^2$가 짝수이므로 2로 나눌 수 있다. ($2|a^2$)
$a^2 \text{ is even} (2|a^2)\\
a \text{ is even} (2|a)\\
4|a^2\\
4|2b^2\\
2|b\\
2|b (b \text{ is even})$
$a$와 $b$가 모두 짝수이므로, $\frac{a}{b}$의 성질인 (더 이상 약분되지 않는 분수)가 깨지게 되고, 이로인해 $\neg p$는 거짓이 된다. $\neg p$가 거짓이므로, $p$는 참이라는 것이 증명된다.
귀납법
어떤 $n$에 대한 바탕 명제Base Case가 참일 때, 이 명제가 $n+1$에도 적용된다는 귀납 명제Induction Rule를 증명하여 무한히 많은 다른 명제들 ($n+2, \cdots n+m$에도 적용되는)도 참임을 증명하는 것이다.
예를들어, 우리가 $p(n)$을 증명하고자 할 때, $\forall n \in \mathbb{N} , p(n) \text{ is True}$임을 밝히려면 아래 바탕 명제와 귀납 명제를 증명하면 된다.
바탕 명제:
$$ p(0) \text{ is True} $$
귀납 명제:
$$ \forall n \geq 0, p(n) \rightarrow p(n+1) \text{ is True} $$
등차수열의 합 공식 귀납법으로 증명하기
$$ P(n): \forall n \geq 0, \sum^{n}_{i=1} i =\frac{n(n+1)}{2} $$
1) Base Case:
$$p(0) = \frac{0(0+1)}{2} = 0 (\text{True}) $$
2) Inductive step:
$$\forall n \geq 0, p(n) \Rightarrow p(n+1) $$
$$\begin{align*}
p(n+1) &= (\sum^{n}_{i=1}i) + n+1\\
&= \frac{n(n+1)}{2}+n+1\\
&= \frac{n(n+1)+2n+2}{2}\\
&= \frac{n^2 + n + 2n + 2}{2}
&= \frac{(n+1)(n+2)}{2} = \text{True}
\end{align*}$$
L 모양 타일들과 하나의 빈 칸으로 $2^n$ 공간 채우기
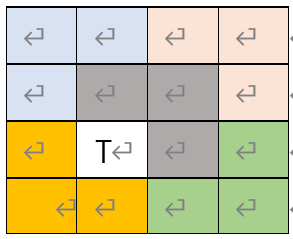
위 그림과 같이, $2^n \times 2^n$ 크기의 공간을 L 모양 타일들과 하나의 빈 칸 T로 채울 수 있음을 증명해보자.
Base Case:
$p(0)$은 $1\times 1$ 공간에 T 하나만 넣으면 되므로 참이다.
Inductive Step:
$2^n\times 2^n$공간을 $2^{n-1}$공간 4개로 나누는 방식으로 해결하면 된다. 최종적으로 $2\times 2$공간이 남는데, 이때 T들을 모아 L 모양을 만들고, 남는 T를 하나 사용하여 증명할 수 있다.
'학부 수업 > 이산수학' 카테고리의 다른 글
| 4. 정수론: 최대공약수 (Number Theory: Great Common Divisor) (1) | 2020.10.14 |
|---|---|
| 3.5 Unstacking Game 강한 귀납법으로 증명하기 (0) | 2020.10.14 |
| 3.5 귀납법을 통한 문자 퍼즐 문제 증명 (0) | 2020.10.14 |
| 3. 좋은 증명과 강한 수학적 귀납법 (Good Proof and Strong Induction) (1) | 2020.10.14 |
| 1. 증명과 명제, 공리 (Proof, Proposition and Axioms) (2) | 2020.09.07 |
댓글
이 글 공유하기
다른 글
-
3.5 Unstacking Game 강한 귀납법으로 증명하기
3.5 Unstacking Game 강한 귀납법으로 증명하기
2020.10.14 -
3.5 귀납법을 통한 문자 퍼즐 문제 증명
3.5 귀납법을 통한 문자 퍼즐 문제 증명
2020.10.14 -
3. 좋은 증명과 강한 수학적 귀납법 (Good Proof and Strong Induction)
3. 좋은 증명과 강한 수학적 귀납법 (Good Proof and Strong Induction)
2020.10.14 -
1. 증명과 명제, 공리 (Proof, Proposition and Axioms)
1. 증명과 명제, 공리 (Proof, Proposition and Axioms)
2020.09.07