4. 행렬의 계수와 기저, 차원 (Rank of Matrix, Basis, Dimension)
어떤 행렬을 행사다리꼴행렬Row Echelon Form로 만들었을 때, 행 전체가 0이 아닌 행의 갯수는 수학적으로 중요한 의미를 가진다. 이 수를 행렬의 계수Rank라 한다.
$$ A = \begin{bmatrix}
1&2&3\\
0&4&5\\
0&0&6\\
0&0&0 \end{bmatrix} $$
예를들어, 위 행렬 $A$의 계수는 3이다.
행렬의 계수는 행렬이 가지는 선형독립/종속의 성질과 관련이 있다. 아래 행렬 $B$를 보자.
$$ B = \begin{bmatrix}
1&-1&3\\
2&-2&6\\
-1&1&-3\end{bmatrix} $$
얼핏 보기에는 3개의 행이 각각 다른 값을 가지고 있는 것처럼 보이지만, 사실 행 2와 행 3은 행 1에 각각 -2, -1을 곱한 값으로, 행 1에 종속되어 있다. 이처럼 행이 다른 행들의 선형 조합으로 표현될 수 있는 경우, 이 관계를 선형 종속Linearly Dependent이라 한다. (1차 종속이라고도 한다.)
반대로 어떤 행이 다른 행들의 선형 조합으로 표현될 수 없는 경우, 이 행은 선형 독립Linearly Independent이라 한다.
행렬의 기본 연산을 통해 위 행렬을 행사다리꼴로 만들면 다음과 같다.
$$ \text{REF}(B) = \begin{bmatrix}
1&-1&3\\
0&0&0\\
0&0&0\end{bmatrix} $$
결국 위 행렬의 계수는, 행렬의 행의 갯수와 관계없이 1이 된다.
즉, 행렬의 계수는 행렬이 가지고 있는 선형 독립인 행들의 갯수이다.
기저Basis와 차원Dimension
직관으로 이해하기
어떤 2차원 공간 위의 한 벡터 $v$를 다른 벡터들의 선형 결합으로 표현해보자.

2차원 공간에서 한 벡터를 표현하기 위해서는, 최소 2개의 선형 독립인 벡터가 필요하다. ($v$와 선형 종속인 하나의 벡터를 사용하면, 1차원 공간 상에서의 표현이 되어 버린다.)
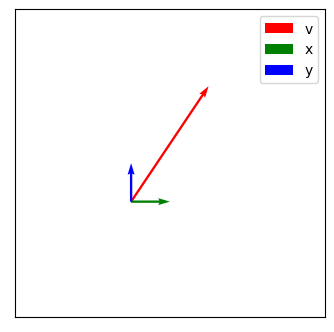
벡터 $v$를 표현하기 위해, 크기가 1인 단위 벡터 $x$와 $y$를 정의했다. 벡터 $v$는 $2x+3y$로 나타낼 수 있다.

선형 독립인 벡터 $x$와 $y$의 결합으로 벡터 $v$를 표현했다. 그런데, 만약 벡터 $x$와 $y$가 선형 종속의 관계를 갖는다면 어떻게 될까?

위 이미지에서는, 벡터 $x=2y$로 $x$와 $y$가 선형 종속의 관계를 갖는다. 결국, 선형 종속인 두 벡터 $x$와 $y$를 이용해서는 2차원 공간 위의 벡터 $v$를 나타낼 수 없다.
기저와 차원의 이해
기저란, 어떤 벡터 공간을 선형 생성하는 선형독립인 벡터들을 말한다. 기저의 조합을 통해, 해당 기저가 생성한 벡터 공간 위의 모든 벡터($v$같은)를 표현할 수 있다. 즉, 위 예시에서 기저는 벡터 $x$와 $y$를 의미한다.
차원이란, 어떤 벡터 공간을 구성하기 위해 필요한 벡터의 수이다. 즉, 어떤 공간이 갖는 기저의 갯수이다.
위 예시에서, 첫번째 경우($x$와 $y$가 선형 독립인 경우) $x$와 $y$를 이용하여 2차원 공간 위에 있는 $v$를 성공적으로 표현할 수 있었다.
$$ A = \begin{bmatrix}
1&0\\
0&1\\
2&3\end{bmatrix}$$
이는 위 행렬 $A$에서, 행 1과 행 2를 이용해 행 3을 나타낸 것과 같다. 즉, 행렬의 계수는 해당 행렬이 만들 수 있는 벡터 공간의 차원과 같다.
'학부 수업 > 선형대수학' 카테고리의 다른 글
| 6. 역행렬 (Inverse Matrix) (0) | 2020.10.05 |
|---|---|
| 5. 행렬식과 여인수 (Determinant and Cofactor) (0) | 2020.10.04 |
| 3. 행렬의 연산과 다양한 특수 행렬들 (0) | 2020.09.14 |
| 2. 선형 방정식의 소거법 (Elimination Method of Linear Equations) (0) | 2020.09.10 |
| 1. 선형 대수와 선형 시스템 (Linear Algebra and Linear System) (2) | 2020.09.10 |
댓글
이 글 공유하기
다른 글
-
6. 역행렬 (Inverse Matrix)
6. 역행렬 (Inverse Matrix)
2020.10.05 -
5. 행렬식과 여인수 (Determinant and Cofactor)
5. 행렬식과 여인수 (Determinant and Cofactor)
2020.10.04 -
3. 행렬의 연산과 다양한 특수 행렬들
3. 행렬의 연산과 다양한 특수 행렬들
2020.09.14 -
2. 선형 방정식의 소거법 (Elimination Method of Linear Equations)
2. 선형 방정식의 소거법 (Elimination Method of Linear Equations)
2020.09.10