6.SOP, POS 단순화와 카르노 맵 (Karnaugh Map)
Canonical Form
지난 강의에서 배웠듯, 불 연산을 SOP나 POS로 나타내는 것을 Canonical Form이라 한다.
- Sum of product form(SOP)
- 변수들을 곱하고(AND) 이 것들을 모두 더한다(OR).
- $ \text{eg:} f = AB + CDE $
- Product of sum(POS)
- 변수들을 더하고(OR) 이들을 곱한다(AND).
- $ \text{eg:} f = (A+B)(C+D+E) $
- 드 모르간 법칙을 이용하면 두 표현을 서로 바꿀 수 있다.
Canonical Form은 효율적이지 않지만 때때로 분석과 디자인에 용이할 때가 있다. Canonical Form의 장점은 모든 변수들이 어떻게 변화하는지 알 수 있다는 것이다. 각 변수는 생략될 때가 많지만 아래와 같이 복원할 수 있다.
$\begin{align*} f(A,B,C) &= AB + BC\\ &= AB(C+\overline{C}) + (A+\overline{A})BC\\ &= ABC + AB\overline{C} + ABC + \overline{A}BC\\ &= ABC + AB\overline{C} + \overline{A}BC \end{align*}$
SOP와 POS는 진리표에서 함수값이 각각 TRUE/FALSE를 갖는 행들의 합으로 표기할 수도 있다.
$f = \Sigma(3,6,7)$
진리표로 회로 설계하기
변수 3개를 갖는 아래 진리표를 이용해 논리 회로를 설계해보자.
| $A$ | $B$ | $C$ | $x$ | SOP Expression |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | $\overline{A}BC$ |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | $A\overline{B}C$ |
| 1 | 1 | 0 | 1 | $AB\overline{C}$ |
| 1 | 1 | 1 | 1 | $ABC$ |
- 진리표의 출력이 1인 행마다 각 변수를 AND 한 minterm을 적어준다.
- 출력을 SOP 형식으로 적어준다.
$$x = \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC$$ - 식을 단순화 해준다.
$$\begin{align*}x &= \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC\\ &= \overline{A}BC + ABC + A\overline{B}C + ABC + AB\overline{C} + ABC\\ &= BC(\overline{A} + A) + AC(\overline{B} + B) + AB(\overline{C} + C)\\ &= BC + AC + AB\end{align*}$$
카르노 맵Karnaugh Map
지금까지는 복잡한 회로를 단순화하기 위해 불 대수의 법칙들을 활용했다. (교환 법칙, 드 모르간 법칙 등의 응용) 논리 회로 단순화를 위한 또 다른 방법으로 카르노 맵, K-맵이 있다.
카르노 맵은 진리표를 기반으로 그린다.
| row | $x$ | $y$ | 식 |
| 0 | 0 | 0 | $\overline{x}\overline{y}$ |
| 1 | 0 | 1 | $\overline{x}y$ |
| 2 | 1 | 0 | $\overline{y}$ |
| 3 | 1 | 1 | $xy$ |
| $\overline{y}$ | $y$ | |
| $\overline{x}$ | 00 0 |
01 1 |
| $x$ | 10 2 |
11 3 |
카르노 맵의 각 셀들은 가능한 모든 조합의 경우를 표기한다.
3개의 변수를 갖는 카르노 맵
| $\overline{y}\overline{z}$ | $\overline{y}z$ | $yz$ | $y\overline{z}$ | |
| $\overline{x}$ | 000 0 |
001 1 |
011 3 |
010 2 |
| $x$ | 100 4 |
101 5 |
111 7 |
110 6 |
이 때, 수평/수직으로 이동할 때 오직 하나의 변수만이 변화한다.
카르노 맵의 단순화
과정
- K-맵을 만들고 진리표에 따라 1과 0을 넣는다.
- 다른 1들과 이웃하지 않는 격리된 1들을 묶는다. (single loops)
- 하나의 1과 이웃하는 1들을 찾아 묶는다. (double loops)
이때, 양 끝의 셀들은 서로 이웃해 있다. (아래 예시의 주황색 묶음 참고) - $2^n$개의 1들이 이웃해 있는 그룹을 찾아 묶는다.
아래 예시의 초록색 묶음 참고 - 이제 겹치는 그룹들을 없에되, 최소한의 항을 남기는 것을 목표로 한다.
- 아직 그룹에 속해있지 않은 1이 있으면 single loop로 묶는다.
아래 파란색 묶음 참고 - 그룹들을 최소한으로 남겼으면 적절히 OR나 AND로 묶는다.
예시
| $\overline{y}\overline{z}$ | $\overline{y}z$ | $yz$ | $y\overline{z}$ | |
| $\overline{w}\overline{x}$ | 0000 | 0001 | 0011 |
0010 $1$ |
| $\overline{w}x$ | 0100 |
0101 $1$ |
0111 $1$ |
0110 |
| $wx$ | 1100 |
1101 $1$ |
1111 $1$ |
1101 |
| $w\overline{x}$ |
1000 $1$ |
1001 | 1011 |
1010 $1$ |
위 K-맵을 단순한 SOP로 나타내면 아래와 같다.
$f = w'xy'z + w'xyz + wxy'z + wxyz + w'x'yz' + wx'y'z' + wx'yz'$
이를 묶어진 그룹을 통해 간소화하면 아래와 같다.
$f = wx'y'z' + xz + yz'$
무관항 처리
때때로 일부 조합이 절대 일어나지 않거나, 무슨 결과를 갖더라도 무관한 경우가 있다. 이런 항을 무관항 또는 "don't care"라 부르고 X로 표시한다.
X는 K-맵에서 필요에 따라 1로 쓸 수도 있으나, 꼭 그룹에 들어가지 않아도 된다.
| $\overline{A}$\overline{B}$ | $\overline{A}B$ | $AB$ | $A\overline{B}$ | |
| $\overline{C}$ | X (얘는 버리고) | 0 | 1 | X (얘는 취한다.) |
| $C$ | 0 | 0 | 1 | 1 |
POS의 K-맵
Sum of product가 아닌 Product of sum 형식으로 K-맵을 응용할 때는 그룹을 0끼리 지어준다는 것만 신경쓰면 된다.
5 변수 카르노 맵
5개의 변수를 갖는 카르노 맵은 4변수 카르노 맵 위에 하나의 카르노 맵을 더 쌓는 것으로 이해할 수 있다.
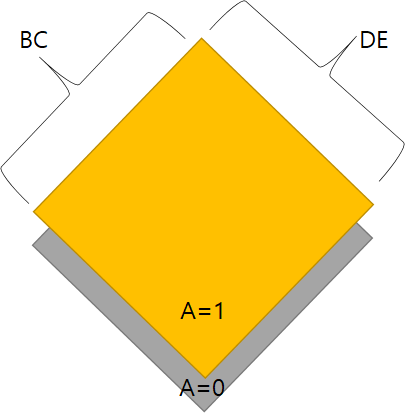
5 변수 카르노 맵의 그룹
5 변수 카르노 맵에서는 상하좌우에 인접한 1 뿐만 아니라 겹쳐진 카르노 맵과의 인접도 고려해야 한다.

'학부 수업 > 디지털시스템' 카테고리의 다른 글
| 8. 조합 회로의 분석 (Combinational Circuit) (0) | 2020.04.24 |
|---|---|
| 7. 범용 게이트 (Universal Gates) (0) | 2020.04.24 |
| 5. 불 대수 (Boolean Algebra) (0) | 2020.04.11 |
| 4. 디지털 논리 회로 (Logic Gates) (0) | 2020.04.11 |
| 3. 부동소수점을 활용한 실수 표현 (IEEE 754 Standard Float) (0) | 2020.04.11 |
댓글
이 글 공유하기
다른 글
-
8. 조합 회로의 분석 (Combinational Circuit)
8. 조합 회로의 분석 (Combinational Circuit)
2020.04.24 -
7. 범용 게이트 (Universal Gates)
7. 범용 게이트 (Universal Gates)
2020.04.24 -
5. 불 대수 (Boolean Algebra)
5. 불 대수 (Boolean Algebra)
2020.04.11 -
4. 디지털 논리 회로 (Logic Gates)
4. 디지털 논리 회로 (Logic Gates)
2020.04.11