1. 선형 대수와 선형 시스템 (Linear Algebra and Linear System)
선형Linear이란, 집합 $A$의 원소 $x_1,x_2, \cdots x_n$에 어떤 상수 $a_1, a_2, \cdots a_n$을 곱하여 더한(선형 결합한) $a_1x_1 + a_2x_2 \cdots a_nx_n$이 집합 $A$에 속하는 경우를 얘기한다.
선형 결합Linear Combination
선형 결합이란, 대응하는 계수와 변수를 모두 곱하여 더한 값을 의미한다.
$$ a_1x_1 + a_2x_2 + a_3x_3 + \cdots + a_nx_n $$
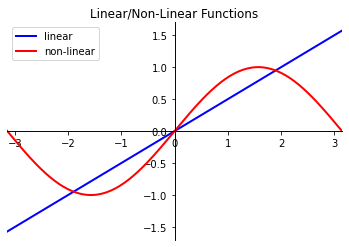
선형/비선형 함수Linear, Non-Linear Functions
일차 함수를 비롯하여 기울기가 변화하지 않는 함수들은 선형 함수, 2차, 3차 함수나 파동 함수와 같이 기울기가 변화하는 함수는 비선형 함수이다.
선형 시스템Linear System
$ a_1x_1 + a_2x_2 = b $와 같은 변수variable $x$와 계수coefficient $a$에 대한 방정식을 선형 방정식Linear Equation이라 한다.
변수 $x_1, x_2, \cdots x_n$에 관한 유한개의 선형 방정식의 집합을 선형 시스템이라 한다. $ x_1=s_1, x_2=s_2, \cdots x_n=s_n$이 선형 시스템 내의 모든 선형 방정식의 해일 때, 이를 선형 시스템의 해라고 하고, 선형 시스템의 모든 해의 집합을 해집합이라 한다.
선형 시스템에서 어떤 방정식들이 같은 해를 공유하면, 이를 두 식이 동치equivalent라 한다.
동차선형시스템Homogeneous System
선형 시스템의 모든 방정식이 $b_1 = b_2 = \cdots = b_n = 0$을 만족할 떄, 이 시스템을 동차선형시스템이라 부른다. 동차선형시스템에서 $x_1=x_2=\cdots = x_n = 0$은 항상 해가 되는데, 이러한 경우를 자명해Trivial Solution라 한다. 한편, 동차선형시스템에서 $x$ 중 하나라도 0이 아닌 해가 있을 때 이 해는 비자명해Nontrivial Solution라 부른다.
'학부 수업 > 선형대수학' 카테고리의 다른 글
| 6. 역행렬 (Inverse Matrix) (0) | 2020.10.05 |
|---|---|
| 5. 행렬식과 여인수 (Determinant and Cofactor) (0) | 2020.10.04 |
| 4. 행렬의 계수와 기저, 차원 (Rank of Matrix, Basis, Dimension) (0) | 2020.10.04 |
| 3. 행렬의 연산과 다양한 특수 행렬들 (0) | 2020.09.14 |
| 2. 선형 방정식의 소거법 (Elimination Method of Linear Equations) (0) | 2020.09.10 |
댓글
이 글 공유하기
다른 글
-
5. 행렬식과 여인수 (Determinant and Cofactor)
5. 행렬식과 여인수 (Determinant and Cofactor)
2020.10.04 -
4. 행렬의 계수와 기저, 차원 (Rank of Matrix, Basis, Dimension)
4. 행렬의 계수와 기저, 차원 (Rank of Matrix, Basis, Dimension)
2020.10.04 -
3. 행렬의 연산과 다양한 특수 행렬들
3. 행렬의 연산과 다양한 특수 행렬들
2020.09.14 -
2. 선형 방정식의 소거법 (Elimination Method of Linear Equations)
2. 선형 방정식의 소거법 (Elimination Method of Linear Equations)
2020.09.10